online travel distance calculator

• Coordinates
• Language (EN)

Map Distance Calculator

Note: To measure the distance on the google maps distance calculator tool. First zoom in, or enter the address of your starting point. Then draw a route by clicking on the starting point, followed by all the subsequent points you want to measure. You can calculate the length of a path, running route, fence, border, or the perimeter of any object that appears on a google map. The distance calculator will then display a measurement of the length in feet, meters, miles and kilometers.

Share using this link

Distance Converters

Distance Calculator

The distance calculator app helps you find the mileage between cities and compare distances by road or air. You can also check how far it is from your current location to any city. Calculate your travel distance between cities quickly and easily using this tool.

Please enable JavaScript

Recent Places

Distance Calculator Between Cities for Precise Driving Distances

Efficiently find the distance between cities, including driving distances, estimated travel times, and detailed route maps for any journey in the USA, from cross-country adventures to short drives.

This distance calculator, covering the United States, North America, and worldwide, simplifies your travel planning. Enter your start and end points in the "From" and "To" fields — accepting city names, addresses, or GPS coordinates — and click "Calculate" to get started.

Customize your journey with "Fuel consumption" and "Fuel price" for cost estimates, and use the crosshair icon for map selections. Dive into "Advanced options" to add stops or adjust speeds, tailoring the trip to your pace and ensuring accurate travel time predictions.

Driving Distance Between Two Cities: US Route Examples

• Distance from Dallas to Houston
• Distance from Austin to Houston
• Distance from Seattle to Portland
• Distance from Dallas to San Antonio
• Distance from San Francisco to Sacramento
• Distance from San Francisco to San Diego
• Distance from Dallas to Chicago
• Distance from Houston to New Orleans
• Distance from Denver to Chicago
• Distance from New York to Chicago

Route Planner for Estimating Distance Between Two Points

Family Vacation Planning : Families planning summer vacations can use the distance calculator to plan their route, estimate fuel costs based on their car's fuel consumption, and calculate budget needs, ensuring a cost-effective and enjoyable journey.

Business Travel Optimization : Professionals can plot the most efficient routes for their business trips, incorporating distance calculations to manage time effectively and budget for travel expenses accurately.

Logistics and Freight Management : Long-haul truckers and freight forwarders can utilize the tool to map out routes between cities, estimate mileage, and calculate transportation costs based on company tariffs, optimizing delivery schedules and pricing.

Meeting Halfway : Friends living in different cities can find a central meeting point by calculating the halfway distance between their locations, making it easier to arrange reunions and share new adventures together.

Explore Functions of the City-to-City Distance Calculator

City distances evolve annually with the construction of new roads, highways, and bridges.

Our online Distance Between Cities Calculator complements your preferred GPS navigator by allowing you to map out your route in advance, while your GPS assists during the drive.

The calculator utilizes OSM data and incorporates key Google Maps functionalities, including:

• Viewing distances and routes on a map for a comprehensive journey overview.
• Interactive map features like zoom, drag-and-drop, and full-screen mode.
• Route customization by adjusting markers directly on the map or adding stops via addresses.
• Distance calculations in either kilometers or miles, with unit preferences adjustable in the menu.

Exclusive features of our calculator include:

• The ability to print, save as PDF/PNG, or export routes to GIS and GPS formats such as GPX, KML, and GeoJSON .
• A route scheme offering a sequence of cities and timing for passing intermediate cities, an efficient alternative to detailed turn-by-turn directions for long distances.
• Fuel cost estimation adaptable to various fuel types. Just input your vehicle's fuel efficiency.
• Capability to generate distance matrices, savable in Excel format, for comprehensive planning.

USA, North America, and Worldwide Coverage

138,192 localities covered in United States. 1,971,411 localities worldwide.

This service measures the distance between cities around the world and is available in several languages:

• English ca.drivebestway.com Canada Mileage Calculator
• Spanish www.mejoresrutas.com Traza tu ruta por México
• Portuguese www.melhoresrotas.com Calculadora de distância entre cidades do Brasil
• English au.drivebestway.com Aussie Distance Calculator
• English gb.drivebestway.com UK Road Distance Calculator
• Spanish es.mejoresrutas.com Calcular ruta entre ciudades españolas
• Spanish ar.mejoresrutas.com Calcular distancia entre ciudades argentinas
• Spanish co.mejoresrutas.com Calcular distancia entre ciudades colombianas
• Spanish us.mejoresrutas.com Calcular distancia entre ciudades de EE. UU.
• Spanish cl.mejoresrutas.com Calcular km entre ciudades chilenas
• Spanish pe.mejoresrutas.com Distancia entre dos puntos en Perú
• Spanish ve.mejoresrutas.com Distancia entre dos puntos en Venezuela
• Spanish br.mejoresrutas.com Distancia entre ciudades brasileñas
• Portuguese pt.melhoresrotas.com Calculadora de distância entre cidades em Portugal
• French www.bonnesroutes.com Calculateur de distance France
• French ca.bonnesroutes.com Calculateur de distance Canadien
• German www.besterouten.com Routenplaner Deutschland
• Polish www.najlepszetrasy.com Kalkulator odległości drogowych w Polsce
• Czech www.dobracesta.com Kalkulačka vzdálenosti mezi českými městy
• Italian www.percorsomigliore.com Calcola distanze chilometriche in Italia
• Malay www.pandujalanterbaik.com Pengiraan jarak antara bandar di Malaysia
• Dutch www.besteroutes.com Afstand meten in Nederland
• Turkish www.duzgunyolusec.com Türkiye şehirler arası mesafe hesaplama
• Dutch be.besteroutes.com Afstand berekenen tussen Belgische steden
• German be.besterouten.com Routenplaner Belgien Auto
• French be.bonnesroutes.com Calculateur de distance belge
• French ch.bonnesroutes.com Calculateur de distance Suisse
• German ch.besterouten.com Routenplaner Schweiz
• German at.besterouten.com Routenplaner Österreich

How Driving Distance Is Calculated Between Two Locations

Algorithm for calculating driving distances between cities.

This route calculation tool harnesses the power of shortest path search algorithms within a weighted road graph, employing sophisticated algorithms like Dijkstra, A-Star, and Contraction Hierarchies . Unlike conventional calculators that use distance or travel time as the graph weight, our system optimizes drive time for vehicles, favoring routes on higher-class roads for a smoother journey.

The backbone of this tool is built on OpenStreetMap data, ensuring our road graphs are accurate and up-to-date. We calculate distances between road segments with the haversine formula , using precise GPS coordinates to measure the Great Circle Distance. This formula is pivotal for calculating "air distance" or "straight line distance" between two points, taking into account the curvature of the Earth.

Road distances, however, diverge from straight line distances due to the natural curvature and layout of roads . To address this, roads are represented as segmented lines, and the haversine formula is applied to each segment, allowing for precise calculation of the journey length between any two points.

Recognizing that cities encompass large areas, our tool selects a central point within each city for distance calculations between cities. For personalized route planning, users can specify exact addresses or select points on the map. Additionally, the route's start and end points can be adjusted directly on the map for enhanced customization.

Travel time calculations break down the route into segments, evaluating the maximum permitted speed for each segment to estimate the fastest possible travel time.

It’s important to note that while our route calculation relies on advanced computer modeling for accuracy, no model is perfect. We encourage users to plan with a margin for adjustment to ensure a reliable and efficient journey.

Alternative Methods for Distance Calculation Between Two Addresses

One simple way to measure distance is by using a highway atlas. By tracing a route with your eye and rolling a curvimeter along it, you can gauge the distance. Estimating travel time involves assuming an average speed of 50 miles/hour on major intercity roads. Although this method provides rough estimates, it's straightforward.

In the absence of a curvimeter, a ruler can serve as a substitute. Start by aligning the ruler's zero mark with your route's beginning and follow the road's bends closely. Then, translate the measured length into kilometers or miles using the map's scale, which is typically provided in the atlas.

For those seeking a more streamlined approach, pre-calculated distance tables specifically for the USA are available on websites, atlases, and guidebooks. Particularly useful for journeys between major cities, these tables streamline planning, although they may omit smaller locales.

• Widget for Website
• Popular routes
• Suggest idea

Distance Calculator

Distance calculation introduction.

The distance value in red color indicates the air (flying) distance, also known as great circle distance .

As you start to write the name of a city or place, distance calculator will suggest you place names automatically, you may choose from them to calculate distance . You can also list the countries and the cities in them, to calculate the distance between cities.

Start Location : is the starting point of route, where the distance calculation start from, origin city or place name. End Location : is the end point of route, where the distance calculation end, destination city or place name. Distance Unit : is the unit of distance, you can choose kilometers, miles or meters. Calculator will immediately calculate with selected distance unit. Kilometers (km): is the unit of length equal to 1000 meters or 0.62137 miles. Miles (mi): is also the unit of length which is rarely used and is equal to 1.60934 kilometers.

Distance Between Cities

List of distances from major cities.

Follow us on

Country Distances

Visit the country page to calculate distance between cities.

• United States
• Philippines
• Democratic Republic of the Congo
• United Kingdom
• South Africa
• South Korea

Recent Comments

Quite informative. Thanks.

Dude, please! Remove the openstreetmap and switch back to Google Maps. That openstreetmap is really disgusting and annoying.

I love it it is so fun!!!

Very good service I like it

it's not distance rather displacement(shortest distance) , no matter if any river coming the way.

I wis it had morer options like walking driving and buses

I’m not a pilot nor do I fly. Airlines do not fly by this planner either. It gives you general directions from point A to Point B. That’s about it folks.

It is a very useful to manage the travel plan

The website is very useful to have an idea of distances between cities. Wish if it gives the road distances!

This is a very helpful website to use! Thanks so much!

amazing tool

Thank you for this map. Wish I could print it

With no delays can travel 50 - 60 miles in 1hhour also depends on traffic delays

Car Road distances please.

Please include miles by boat...

this is an amazing site 10/10!

Awesome tool!

It would ideal if map is shown with route , distance condition of the road, time taken and useful information

Thank you for this calculator

Distance From To - Calculate distance between two addresses, cities, states, zipcodes, or locations

Enter a city, a zipcode, or an address in both the Distance From and the Distance To address inputs. Click Calculate Distance, and the tool will place a marker at each of the two addresses on the map along with a line between them. The distance between them will appear just above the map in both miles and kilometers. The tool is useful for estimating the mileage of a flight, drive, or walk. Can easily determine the distance between 2 cities as well.

Other tools to help with distance questions

In addition to this tool we also offer a couple other tools that can help find the distance on a map. You can use the mileage calculator to compare the difference between driving or flying between 2 cities. If on the other hand you want to click multiple points on the map in order to find the distance of the entire line you can do that with the distance calculator . We are always trying to find better ways to provide you with the information you need. If you have a suggestion please let us know.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Given Points
• Given Slope & Point
• Slope Intercept Form
• Start Point
• Parallel Lines
• Perpendicular
• Perpendicular Lines
• Perpendicular Slope
• Is a Function
• Domain & Range
• Slope & Intercepts
• Periodicity
• Domain of Inverse
• Critical Points
• Inflection Points
• Monotone Intervals
• Extreme Points
• Global Extreme Points
• Absolute Extreme
• Turning Points
• End Behavior
• Average Rate of Change
• Piecewise Functions
• Discontinuity
• Values Table
• Compositions
• Arithmetics
• Circumference
• Eccentricity
• Conic Inequalities
• Transformation
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• distance\:(-3\sqrt{7},\:6),\:(3\sqrt{7},\:4)
• distance\:(-5,\:8d),\:(0,\:4)
• distance\:(-2,\:-3),\:(-1,\:-2)
• distance\:(p,\:1),\:(0,\:q)
• distance\:(3\sqrt{2},7\sqrt{5})(\sqrt{2},-\sqrt{5})
• distance\:(-2,-3),(-1,-2)

distance-calculator

• Slope, Distance and More Ski Vacation? Nope, this is serious stuff; it’s about finding the slope of a line, finding the equation of a line...

Please add a message.

Message received. Thanks for the feedback.

Speed, Distance & Time Calculator

Use this speed calculator to easily calculate the average speed, distance travelled and the trip duration of a vehicle: car, bus, train, bike, motorcycle, plane etc. Works with miles, feet, kilometers, meters, etc..

Related calculators

• Speed, Distance & Time Calculation
• Average Speed formula
• Distance formula
• Duration (Time) formula
• How to calculate the average speed of a car?

    Speed, Distance & Time Calculation

In order to use the above speed, distance & time calculator, or do such math on your own, you will need to know two out of three metrics: speed, distance, time. You will need to convert the metrics to the same time and distance units, e.g. miles, kilometers, meters, yards, feet, and hours, minutes or seconds. For example, if you have speed in mph (miles per hour), time should also be in hours. If you have distance in kilometers, then speed should also be in km/h (kilometers per hour).

The unit of the result will depend on the units you input, but our speed calculator will conveniently display additional units where appropriate.

    Average Speed formula

The formula for average speed, also called average velocity in physics and engineering, is:

where v is the velocity, d is the distance, and t is the time, so you can read it as Speed = Distance / Time . As noted above, make sure you convert the units appropriately first, or use our speed calculator which does that automatically. The resulting unit will depend on the units for both time and distance, so if your input was in miles and hours, the speed will be in mph. If it was in meters and seconds, it will be in m/s (meters per second).

Example: If you took a plane from New York to Los Angeles and the flight was 5 hours of air time, what was the speed of the plane, given that the flight path was 2450 miles? The answer is 2450 / 5 = 490 mph (miles per hour) average speed. If you want the result in km/h, you can convert from miles to km to get 788.58 km/h.

    Distance formula

The formula for distance, if you know time (duration) and the average speed, is:

Example: If a truck travelled at an average speed of 80 km per hour for 4 hours, how many miles did it cover in that time? To find the miles covered, first, calculate 80 * 4 = 320 km, then convert km to miles by dividing by 1.6093 or by using our km to miles converter to get the answer: 198.84 miles.

    Duration (Time) formula

The time, or more precisely, the duration of the trip, can be calculated knowing the distance and the average speed using the formula:

where d is the distance travelled, v is the speed (velocity) and t is the time, so you can read it as Time = Distance / Speed . Make sure you convert the units so both their distance and time components match, or use our trip duration calculator above which will handle conversions automatically. For example, if you have distance in miles and speed in km/h, you will need to convert speed to mph or distance to kilometers. The time unit of the result will match the time unit of the speed measure, so if it is measured in something per hour, the result will be in hours. If it is measured in some unit per second, the result will be in seconds.

Example: If a train can travel 500 miles with an average speed of 50 miles per hour, how long it would take it to complete a 500-mile route? To find the answer, use the formula and substitute the values, resulting in 500 / 50 = 10 hours.

    How to calculate the average speed of a car?

Say you travelled a certain distance with a car or another vehicle and you want to calculate what its average speed was. The easiest way to do that would be by using the calculator above, but if you prefer, you can also do the math yourself. Either way, you need to know the distance to a satisfactory approximation, for which you can use a map (e.g. Google Maps) to measure the distance from point to point. Make sure you measure closely to the path you took, and not via a straight line, unless you travelled by air in which case that would be a good approximation. Of course, having a GPS reading of the distance would be more precise. Then you need to know the travel time. Make sure you subtract any rests or stops you made from the total trip duration.

If the total distance travelled was 500 miles and the time it took you was 5 hours, then your average speed was 500 / 5 = 100 miles per hour (mph). If the distance was 300 kilometers and it took you 5 hours to cover it, your speed was 300 / 5 = 60 km/h (kilometers per hour).

Cite this calculator & page

If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "Speed Distance Time Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/speed-calculator.php URL [Accessed Date: 30 Apr, 2024].

     Transportation calculators

Distance Calculator

The calculators below can be used to find the distance between two points on a 2D plane or 3D space. They can also be used to find the distance between two pairs of latitude and longitude, or two chosen points on a map.

2D Distance Calculator

Use this calculator to find the distance between two points on a 2D coordinate plane.

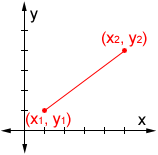
3D Distance Calculator

Use this calculator to find the distance between two points on a 3D coordinate space.

Distance Based on Latitude and Longitude

Use this calculator to find the shortest distance (great circle/air distance) between two points on the Earth's surface.

• Degree-Minute-Second

Distance on Map

Click the map below to set two points on the map and find the shortest distance (great circle/air distance) between them. Once created, the marker(s) can be repositioned by clicking and holding, then dragging them.

Distance in a coordinate system

Distance in a 2D coordinate plane:

The distance between two points on a 2D coordinate plane can be found using the following distance formula

d = √ (x 2 - x 1 ) 2 + (y 2 - y 1 ) 2

where (x 1 , y 1 ) and (x 2 , y 2 ) are the coordinates of the two points involved. The order of the points does not matter for the formula as long as the points chosen are consistent. For example, given the two points (1, 5) and (3, 2), either 3 or 1 could be designated as x 1 or x 2 as long as the corresponding y-values are used:

Using (1, 5) as (x 1 , y 1 ) and (3, 2) as (x 2 , y 2 ):

Using (3, 2) as (x 1 , y 1 ) and (1, 5) as (x 2 , y 2 ):

In either case, the result is the same.

Distance in a 3D coordinate space:

The distance between two points on a 3D coordinate plane can be found using the following distance formula

d = √ (x 2 - x 1 ) 2 + (y 2 - y 1 ) 2 + (z 2 - z 1 ) 2

where (x 1 , y 1 , z 1 ) and (x 2 , y 2 , z 2 ) are the 3D coordinates of the two points involved. Like the 2D version of the formula, it does not matter which of two points is designated (x 1 , y 1 , z 1 ) or (x 2 , y 2 , z 2 ), as long as the corresponding points are used in the formula. Given the two points (1, 3, 7) and (2, 4, 8), the distance between the points can be found as follows:

Distance between two points on Earth's surface

There are a number of ways to find the distance between two points along the Earth's surface. The following are two common formulas.

Haversine formula:

The haversine formula can be used to find the distance between two points on a sphere given their latitude and longitude:

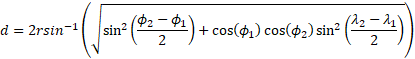
In the haversine formula, d is the distance between two points along a great circle, r is the radius of the sphere, ϕ 1 and ϕ 2 are the latitudes of the two points, and λ 1 and λ 2 are the longitudes of the two points, all in radians.

The haversine formula works by finding the great-circle distance between points of latitude and longitude on a sphere, which can be used to approximate distance on the Earth (since it is mostly spherical). A great circle (also orthodrome) of a sphere is the largest circle that can be drawn on any given sphere. It is formed by the intersection of a plane and the sphere through the center point of the sphere. The great-circle distance is the shortest distance between two points along the surface of a sphere.

Results using the haversine formula may have an error of up to 0.5% because the Earth is not a perfect sphere, but an ellipsoid with a radius of 6,378 km (3,963 mi) at the equator and a radius of 6,357 km (3,950 mi) at a pole. Because of this, Lambert's formula (an ellipsoidal-surface formula), more precisely approximates the surface of the Earth than the haversine formula (a spherical-surface formula) can.

Lambert's formula:

Lambert's formula (the formula used by the calculators above) is the method used to calculate the shortest distance along the surface of an ellipsoid. When used to approximate the Earth and calculate the distance on the Earth surface, it has an accuracy on the order of 10 meters over thousands of kilometers, which is more precise than the haversine formula.

Lambert's formula is as follows:

where a is the equatorial radius of the ellipsoid (in this case the Earth), σ is the central angle in radians between the points of latitude and longitude (found using a method such as the haversine formula), f is the flattening of the Earth, and X and Y are expanded below.

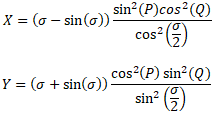
Where P = (β 1 + β 2 )/2 and Q = (β 2 - β 1 )/2

In the expressions above, β 1 and β 1 are reduced latitudes using the equation below:

tan(β) = (1 - f)tan(ϕ)

where ϕ is the latitude of a point.

Note that neither the haversine formula nor Lambert's formula provides an exact distance because it is not possible to account for every irregularity on the surface of the Earth.

What is the distance calculator?

Maps can be difficult to use while planning your trip, with the advances in the internet we wanted to build a free tool that allows you to enter a street name or travel destination and get an exact estimate regarding your journey. Our World map will then plot your route along the road to your chosen destination, this means you can see your directions online. A street map can be seen if you zoom in close enough, this helps you plot your next vacation or important business meeting. It allows you to calculate the distance between town, between cities or even from two street names across the world. There are occasions when the calculator will not be able to predict your journey, this could be if there is no valid route between the points or our service cannot determine the distance based on the given start and end points.

Search a Province

Distance by country, distance calculator in south africa.

This distance calculator is not only for South Africans, anyone from all over the globe is welcome to use the calculator, it was developed as a free tool to calculate the distance between two points. At a later stage we wish to also show the map and its directions, so it will simply show you a text based version of your directions. Each time you enter a start and end point, all you have to do is click [Calculate Distance] This will then take you to another page that will show you your distance and time taken to complete the journey.

Planning your Trip Quickly

Find your destination easier using distancecalculator.co.za.