travelling salesman problem using approximation algorithm program

• Data Structures & Algorithms
• DSA - Overview
• DSA - Environment Setup
• DSA - Algorithms Basics
• DSA - Asymptotic Analysis
• Data Structures
• DSA - Data Structure Basics
• DSA - Data Structures and Types
• DSA - Array Data Structure
• Linked Lists
• DSA - Linked List Data Structure
• DSA - Doubly Linked List Data Structure
• DSA - Circular Linked List Data Structure
• Stack & Queue
• DSA - Stack Data Structure
• DSA - Expression Parsing
• DSA - Queue Data Structure
• Searching Algorithms
• DSA - Searching Algorithms
• DSA - Linear Search Algorithm
• DSA - Binary Search Algorithm
• DSA - Interpolation Search
• DSA - Jump Search Algorithm
• DSA - Exponential Search
• DSA - Fibonacci Search
• DSA - Sublist Search
• DSA - Hash Table
• Sorting Algorithms
• DSA - Sorting Algorithms
• DSA - Bubble Sort Algorithm
• DSA - Insertion Sort Algorithm
• DSA - Selection Sort Algorithm
• DSA - Merge Sort Algorithm
• DSA - Shell Sort Algorithm
• DSA - Heap Sort
• DSA - Bucket Sort Algorithm
• DSA - Counting Sort Algorithm
• DSA - Radix Sort Algorithm
• DSA - Quick Sort Algorithm
• Graph Data Structure
• DSA - Graph Data Structure
• DSA - Depth First Traversal
• DSA - Breadth First Traversal
• DSA - Spanning Tree
• Tree Data Structure
• DSA - Tree Data Structure
• DSA - Tree Traversal
• DSA - Binary Search Tree
• DSA - AVL Tree
• DSA - Red Black Trees
• DSA - B Trees
• DSA - B+ Trees
• DSA - Splay Trees
• DSA - Tries
• DSA - Heap Data Structure
• DSA - Recursion Algorithms
• DSA - Tower of Hanoi Using Recursion
• DSA - Fibonacci Series Using Recursion
• Divide and Conquer
• DSA - Divide and Conquer
• DSA - Max-Min Problem
• DSA - Strassen's Matrix Multiplication
• DSA - Karatsuba Algorithm
• Greedy Algorithms
• DSA - Greedy Algorithms
• DSA - Travelling Salesman Problem (Greedy Approach)
• DSA - Prim's Minimal Spanning Tree
• DSA - Kruskal's Minimal Spanning Tree
• DSA - Dijkstra's Shortest Path Algorithm
• DSA - Map Colouring Algorithm
• DSA - Fractional Knapsack Problem
• DSA - Job Sequencing with Deadline
• DSA - Optimal Merge Pattern Algorithm
• Dynamic Programming
• DSA - Dynamic Programming
• DSA - Matrix Chain Multiplication
• DSA - Floyd Warshall Algorithm
• DSA - 0-1 Knapsack Problem
• DSA - Longest Common Subsequence Algorithm
• DSA - Travelling Salesman Problem (Dynamic Approach)
• Approximation Algorithms
• DSA - Approximation Algorithms
• DSA - Vertex Cover Algorithm
• DSA - Set Cover Problem
• DSA - Travelling Salesman Problem (Approximation Approach)
• Randomized Algorithms
• DSA - Randomized Algorithms
• DSA - Randomized Quick Sort Algorithm
• DSA - Karger’s Minimum Cut Algorithm
• DSA - Fisher-Yates Shuffle Algorithm
• DSA Useful Resources
• DSA - Questions and Answers
• DSA - Quick Guide
• DSA - Useful Resources
• DSA - Discussion
• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Travelling Salesman using Approximation Algorithm

• Travelling Salesman Approximation Algorithm

Implementation

We have already discussed the travelling salesperson problem using the greedy and dynamic programming approaches, and it is established that solving the travelling salesperson problems for the perfect optimal solutions is not possible in polynomial time.

Therefore, the approximation solution is expected to find a near optimal solution for this NP-Hard problem. However, an approximate algorithm is devised only if the cost function (which is defined as the distance between two plotted points) in the problem satisfies triangle inequality .

The triangle inequality is satisfied only if the cost function c, for all the vertices of a triangle u, v and w, satisfies the following equation

It is usually automatically satisfied in many applications.

Travelling Salesperson Approximation Algorithm

The travelling salesperson approximation algorithm requires some prerequisite algorithms to be performed so we can achieve a near optimal solution. Let us look at those prerequisite algorithms briefly −

Minimum Spanning Tree − The minimum spanning tree is a tree data structure that contains all the vertices of main graph with minimum number of edges connecting them. We apply prim’s algorithm for minimum spanning tree in this case.

Pre-order Traversal − The pre-order traversal is done on tree data structures where a pointer is walked through all the nodes of the tree in a [root – left child – right child] order.

Step 1 − Choose any vertex of the given graph randomly as the starting and ending point.

Step 2 − Construct a minimum spanning tree of the graph with the vertex chosen as the root using prim’s algorithm.

Step 3 − Once the spanning tree is constructed, pre-order traversal is performed on the minimum spanning tree obtained in the previous step.

Step 4 − The pre-order solution obtained is the Hamiltonian path of the travelling salesperson.

The approximation algorithm of the travelling salesperson problem is a 2-approximation algorithm if the triangle inequality is satisfied.

To prove this, we need to show that the approximate cost of the problem is double the optimal cost. Few observations that support this claim would be as follows −

The cost of minimum spanning tree is never less than the cost of the optimal Hamiltonian path. That is, c(M) ≤ c(H * ).

The cost of full walk is also twice as the cost of minimum spanning tree. A full walk is defined as the path traced while traversing the minimum spanning tree preorderly. Full walk traverses every edge present in the graph exactly twice. Thereore, c(W) = 2c(T)

Since the preorder walk path is less than the full walk path, the output of the algorithm is always lower than the cost of the full walk.

Let us look at an example graph to visualize this approximation algorithm −

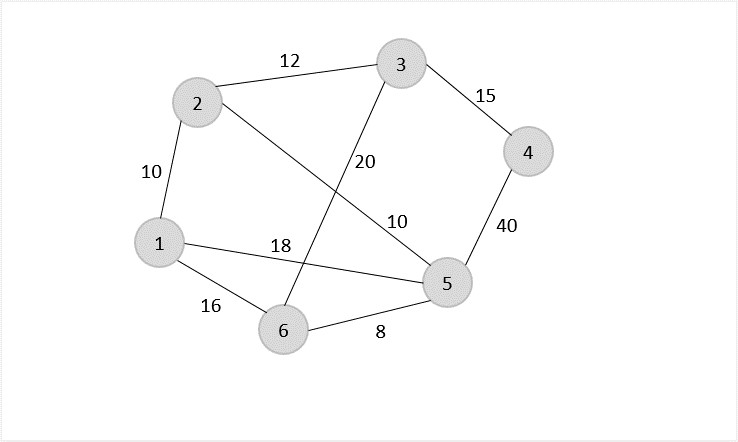
Consider vertex 1 from the above graph as the starting and ending point of the travelling salesperson and begin the algorithm from here.

Starting the algorithm from vertex 1, construct a minimum spanning tree from the graph. To learn more about constructing a minimum spanning tree, please click here.

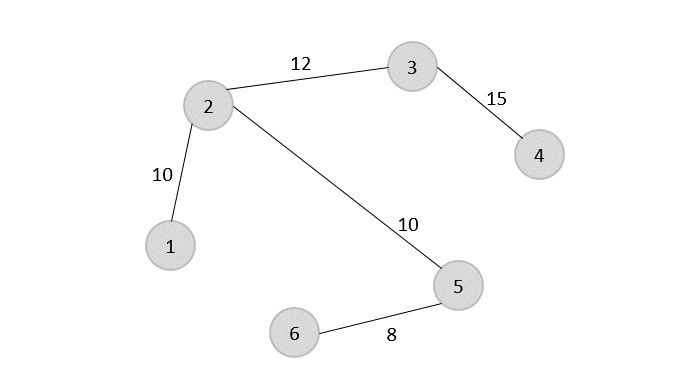
Once, the minimum spanning tree is constructed, consider the starting vertex as the root node (i.e., vertex 1) and walk through the spanning tree preorderly.

Rotating the spanning tree for easier interpretation, we get −

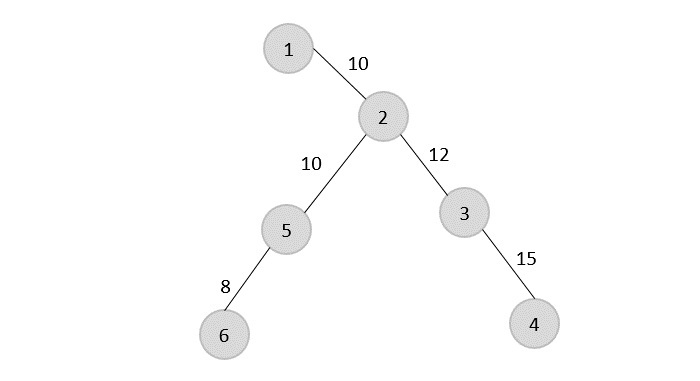
The preorder traversal of the tree is found to be − 1 → 2 → 5 → 6 → 3 → 4

Adding the root node at the end of the traced path, we get, 1 → 2 → 5 → 6 → 3 → 4 → 1

This is the output Hamiltonian path of the travelling salesman approximation problem. The cost of the path would be the sum of all the costs in the minimum spanning tree, i.e., 55 .

Following are the implementations of the above approach in various programming langauges −

Search anything:

Approximation Algorithm for Travelling Salesman Problem

Algorithms approximation algorithm.

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

In this article we will briefly discuss about the Metric Travelling Salesman Probelm and an approximation algorithm named 2 approximation algorithm , that uses Minimum Spanning Tree in order to obtain an approximate path.

What is the travelling salesman problem ?

Travelling Salesman Problem is based on a real life scenario, where a salesman from a company has to start from his own city and visit all the assigned cities exactly once and return to his home till the end of the day. The exact problem statement goes like this, "Given a set of cities and distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point."

There are two important things to be cleared about in this problem statement,

• Visit every city exactly once
• Cover the shortest path

The naive & dynamic approach for solving this problem can be found in our previous article Travelling Salesman Problme using Bitmasking & Dynamic Programming . We would really like you to go through the above mentioned article once, understand the scenario and get back here for a better grasp on why we are using Approximation Algorithms.

If you think a little bit deeper, you may notice that both of the solutions are infeasible as there is no polynomial time solution available for this NP-Hard problem. There are approximate algorithms to solve the problem though.

The approximate algorithms for TSP works only if the problem instance satisfies Triangle-Inequality .

Why are we using triangle inequality ?

So in the above instance of solving Travelling Salesman Problem using naive & dynamic approach, we may notice that most of the times we are using intermediate vertices inorder to move from one vertex to the other to minimize the cost of the path, we are going to minimize this scenario by the following approximation.

Let's approximate that,

"The least distant path to reach a vertex j from i is always to reach j directly from i, rather than through some other vertex k (or vertices)" i.e.,

dis(i, j) <= dis(i, k) + dist(k, j)

dis(a,b) = diatance between a & b, i.e. the edge weight.

The Triangle-Inequality holds in many practical situations.

Now our problem is approximated as we have tweaked the cost function/condition to traingle inequality.

What is the 2 approximation algorithm for TSP ?

When the cost function satisfies the triangle inequality, we may design an approximate algorithm for the Travelling Salesman Problem that returns a tour whose cost is never more than twice the cost of an optimal tour. The idea is to use Minimum Spanning Tree (MST) .

The Algorithm :

• Let 0 be the starting and ending point for salesman.
• Construct Minimum Spanning Tree from with 0 as root using Prim’s Algorithm .
• List vertices visited in preorder walk/Depth First Search of the constructed MST and add source node at the end.

Why 2 approximate ?

Following are some important points that maybe taken into account,

• The cost of best possible Travelling Salesman tour is never less than the cost of MST. (The definition of MST says, it is a minimum cost tree that connects all vertices).
• The total cost of full walk is at most twice the cost of MST (Every edge of MST is visited at-most twice)
• The output of the above algorithm is less than the cost of full walk.

Designing the code:

Step - 1 - constructing the minimum spanning tree.

We will be using Prim's Algorithm to construct a minimum spanning tree from the given graph as an adjacency matrix.

Prim's Algorithm in Brief:

As we may observe from the above code the algorithm can be briefly summerized as,

• Creating a set mstSet that keeps track of vertices already included in MST.
• Assigning a key value to all vertices in the input graph. Initialize all key values as INFINITE . Assign key value as 0 for the first vertex so that it is picked first.
• Pick a vertex u which is not there in mstSet and has minimum key value.( minimum_key() )
• Include u to mstSet.
• Update key value of all adjacent vertices of u. To update the key values, iterate through all adjacent vertices. For every adjacent vertex v, if weight of edge u-v is less than the previous key value of v, update the key value as weight of u-v.

Step - 2 - Getting the preorder walk/ Defth first search walk:

We have two ways to perform the second step, 1 - Costructing a generic tree on the basic of output received from the step -1 2 - Constructing an adjacency matrix where graph[i][j] = 1 means both i & j are having a direct edge and included in the MST.

For simplicity, let's use the second method where we are creating a two dimensional matrix by using the output we have got from the step- 1, have a look at the below code to understand what we are doing properly.

Depth First Search Algorithm:

• Push the starting_vertex to the final_ans vector.
• Checking up the visited node status for the same node.
• Iterating over the adjacency matrix (depth finding) and adding all the child nodes to the final_ans.
• Calling recursion to repeat the same.

It's pretty similar to preorder traversal and simpler to understand, have a look at the following code,

The final_ans vector will contain the answer path.

The Final Code:

An example:.

Let's try to visualize the things happening inside the code,

Let's have a look at the graph(adjacency matrix) given as input,

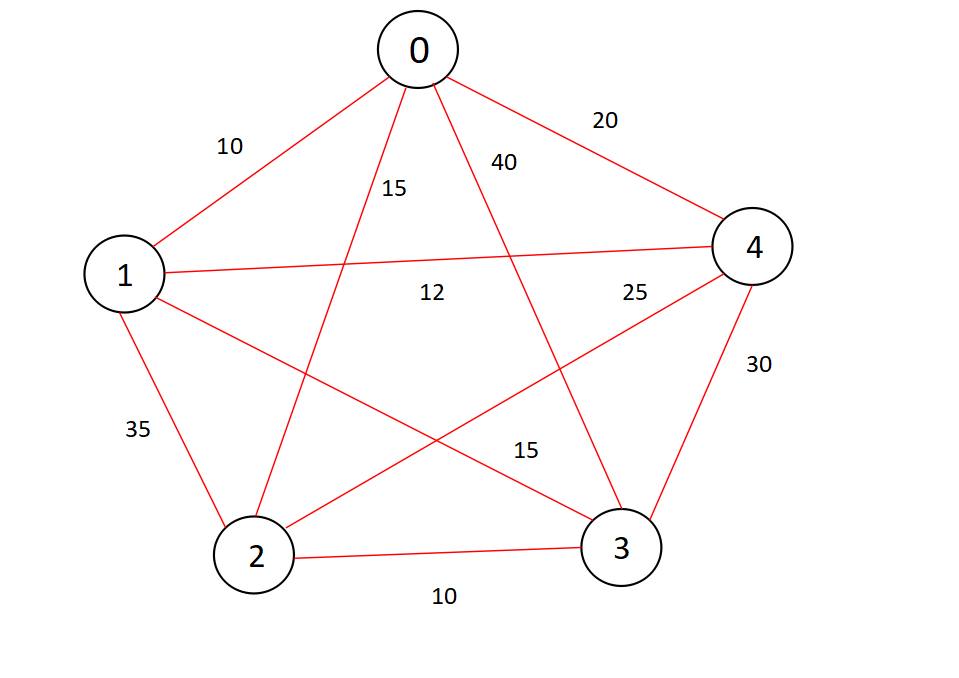
Hence we have the optimal path according to the approximation algorithm, i.e. 0-1-3-4-2-0 .

Complexity Analysis:

The time complexity for obtaining MST from the given graph is O(V^2) where V is the number of nodes. The worst case space complexity for the same is O(V^2) , as we are constructing a vector<vector<int>> data structure to store the final MST.

The time complexity for obtaining the DFS of the given graph is O(V+E) where V is the number of nodes and E is the number of edges. The space complexity for the same is O(V) .

Hence the overall time complexity is O(V^2) and the worst case space somplexity of this algorithm is O(V^2) .

Traveling Salesman Problem: Exact Solutions vs. Heuristic vs. Approximation Algorithms

Last updated: March 18, 2024

• Graph Traversal
• Path Finding
• Metaheuristics
• NP-Complete
• Optimization

1. Introduction

The Traveling Salesman Problem (TSP) is a well-known challenge in computer science, mathematical optimization , and operations research that aims to locate the most efficient route for visiting a group of cities and returning to the initial city. TSP is an extensively researched topic in the realm of combinatorial optimization . It has practical uses in various other optimization problems, including electronic circuit design, job sequencing, and so forth.

This tutorial will delve into the TSP definition and various types of algorithms that can be used to solve the problem. These algorithms include exact, heuristic, and approximation methods.

2. Travelling Salesman Problem

The TSP is often presented as a challenge to determine the shortest route between cities while visiting each city exactly once and returning to the starting city, using a list of cities and the distances between them . The below figures illustrate a TSP instance for several cities in the United States:

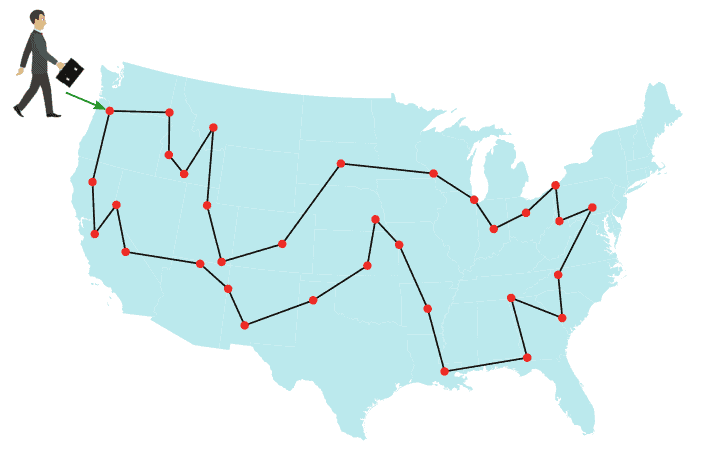
TSP is considered an NP-hard problem , meaning that the time required to find the optimal solution increases exponentially as the number of cities grows . Despite its complexity, the TSP is used in many practical applications, such as optimizing delivery truck routes and scheduling manufacturing processes.

3. Mathematical Formulations

The TSP can be expressed mathematically as an Integer Linear Program (ILP) . There are two well-known formulations of the problem, the Miller-Tucker-Zemlin (MTZ) formulation, and the Dantzig-Fulkerson-Johnson (DFJ) formulation.

The objective in both formulations is to minimize the tour length,

3.1. Miller–Tucker–Zemlin (MTZ) Formulation

In this formulation, constraint (1) mandates that each city must be reached from precisely one other city. Constraint (2) guarantees that from each city, there is a single departure to another city. Lastly, constraints (4) and (5) ensure that there is only one tour that covers all cities and no two or more separate tours that collectively cover all the cities. These constraints are necessary to ensure that the resulting solution is a valid tour of all cities.

3.2. Dantzig–Fulkerson–Johnson (DFJ) Formulation

The DFJ formulation for TSP was published by G. Dantzig, R. Fulkerson, and S. Johnson in the Journal of the Operations Research Society of America in 1954 . Their proposed formulation is described as follows:

4. TSP Algorithms

Researchers have developed several algorithms to solve the TSP, including exact , heuristic , and approximation algorithms.

Exact algorithms can find the optimal solution but are only feasible for small problem instances.

On the other hand, heuristic algorithms can handle larger problem instances but cannot guarantee to find the optimal solution.

Approximation algorithms balance speed and optimality by producing solutions that are guaranteed to be within a specific percentage of the optimal solution.

4.1. Exact Algorithms

The following table summarizes several exact algorithms to solve TSP:

Other approaches include various brand-and-bound algorithms and branch-and-cut algorithms . Branch-and-bound algorithms can handle TSPs with 40-60 cities, while branch-and-cut algorithms can handle larger instances. An example is the Concorde TSP Solver , which was introduced by Applegate et al . in 2006 and can solve a TSP with almost 86,000 cities, but it requires 136 CPU years to do so.

4.2. Heuristics Algorithms

This section will discover some heuristics to solve TSP, including Match Twice and Stitch (MTS) and Lin-Kernighan heuristics . The description of these heuristics are summarized in the below table:

The MTS heuristic consists of two phases . In the first phase, known as cycle construction, two sequential matchings are performed to construct cycles. The first matching returns the minimum-cost edge set with each point incident to exactly one matching edge. Next, all these edges are removed, and the second matching is executed. The second matching repeats the matching process, subject to the constraint that none of the edges chosen in the first matching can be used again. Together, the results of the first and second matchings form a set of cycles. The constructed cycles are stitched together in the second phase to form the TSP tour.

Lin-Kernighan is a local search algorithm and one of the most effective heuristics to solve the symmetric TSP . It takes an existing tour (Hamiltonian cycle) as input and tries to improve it by exploring the neighboring tours to find a shorter one. This process is repeated until a local minimum is reached. The algorithm uses a similar concept as 2-opt and 3-opt algorithms, where the “distance” between two tours is the number of edges that are different between them. Lin-Kernighan builds new tours by rearranging segments of the old tour, sometimes reversing the direction of traversal. It is adaptive and does not have a fixed number of edges to replace in a step, but it tends to replace a small number of edges, such as 2 or 3, at a time.

4.3. Approximation Algorithms

In this section, we’ll discuss two well-known approximation algorithms for TSP, namely the Nearest Neighbor (NN) and the Christofides-Serdyukov algorithms . The description of these algorithms are summarized in the below table:

The Christofides–Serdyukov algorithm is another approximation algorithm for the TSP that utilizes both the minimum spanning tree and a solution to the minimum-weight perfect matching problem . By combining these two solutions, the algorithm is able to produce a TSP tour that is at most 1.5 times the length of the optimal tour. This algorithm was among the first approximation algorithms and played a significant role in popularizing the use of approximation algorithms as a practical approach to solving computationally difficult problems.

5. Applications of TSP

TSP has numerous applications across different fields, including:

• Logistics and supply chain management : The TSP is often used to optimize delivery routes and minimize travel costs for logistics and supply chain management. For example, companies like UPS and FedEx use TSP algorithms to optimize their delivery routes and schedules
• DNA sequencing : The TSP has been used in DNA sequencing to determine the order in which to fragment a DNA molecule to obtain its complete sequence. TSP algorithms can help minimize the number of fragments required to sequence a DNA molecule
• Circuit board design : TSP algorithms can be used to optimize the design of circuit boards, where the goal is to minimize the length of the connections between the components
• Network design : The TSP can be used to design optimal networks for telecommunications , transportation, and other systems. The TSP can help optimize the placement of facilities and routing of traffic in such systems
• Manufacturing and production planning : The TSP can be used in production planning and scheduling to optimize the order in which different tasks are performed, minimize setup times, and reduce production costs
• Robotics : The TSP can be used to optimize the path of a robot as it moves through a series of tasks or objectives. TSP algorithms can help minimize the distance traveled by the robot and reduce the time required to complete the tasks
• Image and video processing : The TSP can be used to optimize the order in which different parts of an image or video are processed. This can help improve the efficiency of image and video processing algorithms

6. Conclusion

TSP is a classic problem in computer science and operations research, which has a wide range of applications in various fields, from academia to industry.

This brief provides an overview of the travelling salesman problem, including its definition, mathematical formulations, and several algorithms to solve the problem, which is divided into three main categories: exact, heuristic, and approximation algorithms.

Traveling Salesman Problem and Approximation Algorithms

One of my research interests is a graphical model structure learning problem in multivariate statistics. I have been recently studying and trying to borrow ideas from approximation algorithms, a research field that tackles difficult combinatorial optimization problems. This post gives a brief introduction to two approximation algorithms for the (metric) traveling salesman problem: the double-tree algorithm and Christofides’ algorithm. The materials are mainly based on §2.4 of Williamson and Shmoys (2011).

1. Approximation algorithms

In combinatorial optimization, most interesting problems are NP-hard and do not have polynomial-time algorithms to find optimal solutions (yet?). Approximation algorithms are efficient algorithms that find approximate solutions to such problems. Moreover, they give provable guarantees on the distance of the approximate solution to the optimal ones.

We assume that there is an objective function associated with an optimization problem. An optimal solution to the problem is one that minimizes the value of this objective function. The value of the optimal solution is often denoted by \(\mathrm{OPT}\).

An \(\alpha\)-approximation algorithm for an optimization problem is a polynomial-time algorithm that for all instances of the problem produces a solution, whose value is within a factor of \(\alpha\) of \(\mathrm{OPT}\), the value of an optimal solution. The factor \(\alpha\) is called the approximation ratio.

2. Traveling salesman problem

The traveling salesman problem (TSP) is NP-hard and one of the most well-studied combinatorial optimization problems. It has broad applications in logistics, planning, and DNA sequencing. In plain words, the TSP asks the following question:

Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?

Formally, for a set of cities \([n] = \{1, 2, \ldots, n \}\), an \(n\)-by-\(n\) matrix \(C = (c_{ij})\), where \(c_{ij} \geq 0 \) specifies the cost of traveling from city \(i\) to city \(j\). By convention, we assume \(c_{ii} = 0\) and \(c_{ij} = c_{ji}\), meaning that the cost of traveling from city \(i\) to city \(j\) is equal to the cost of traveling from city \(j\) to city \(i\). Furthermore, we only consider the metric TSP in this article; that is, the triangle inequality holds for any \(i,j,k\): $$ c_{ik} \leq c_{ij} + c_{jk}, \quad \forall i, j, k \in [n]. $$

Given a permutation \(\sigma\) of \([n]\), a tour traverses the cities in the order \(\sigma(1), \sigma(2), \ldots, \sigma(n)\). The goal is to find a tour with the lowest cost, which is equal to $$ c_{\sigma(n) \sigma(1)} + \sum_{i=1}^{n-1} c_{\sigma(i) \sigma(i+1)}. $$

3. Double-tree algorithm

We first describe a simple algorithm called the double-tree algorithm and prove that it is a 2-approximation algorithm.

Double-tree algorithm Find a minimum spanning tree \(T\). Duplicate the edges of \(T\). Find an Eulerian tour. Shortcut the Eulerian tour.

Figure 1 shows the algorithm on a simple five-city instance. We give a step-by-step explanation of the algorithm.

A spanning tree of an undirected graph is a subgraph that is a tree and includes all of the nodes. A minimum spanning tree of a weighted graph is a spanning tree for which the total edge cost is minimized. There are several polynomial-time algorithms for finding a minimum spanning tree, e.g., Prim’s algorithm , Kruskal’s algorithm , and the reverse-delete algorithm . Figure 1a shows a minimum spanning tree \(T\).

There is an important relationship between the minimum spanning tree problem and the traveling salesman problem.

Lemma 1. For any input to the traveling salesman problem, the cost of the optimal tour is at least the cost of the minimum spanning tree on the same input.

The proof is simple. Deleting any edge from the optimal tour results in a spanning tree, the cost of which is at least the cost of the minimum spanning tree. Therefore, the cost of the minimum spanning tree \(T\) in Figure 1(a) is at most \( \mathrm{OPT}\).

Next, each edge in the minimum spanning tree is replaced by two copies of itself, as shown in Figure 1b. The resulting (multi)graph is Eulerian. A graph is said to be Eulerian if there exists a tour that visits every edge exactly once. A graph is Eulerian if and only if it is connected and each node has an even degree. Given an Eulerian graph, it is easy to construct a traversal of the edges. For example, a possible Eulerian tour in Figure 1b is 1–3–2–3–4–5–4–3–1. Moreover, since the edges are duplicated from the minimum spanning tree, the Eulerian tour has cost at most \(2 , \mathrm{OPT}\).

Finally, given the Eulerian tour, we remove all but the first occurrence of each node in the sequence; this step is called shortcutting . By the triangle inequality, the cost of the shortcut tour is at most the cost of the Eulerian tour, which is not greater than \(2 , \mathrm{OPT}\). In Figure 1c, the shortcut tour is 1–3–2–4–5–1. When going from node 2 to node 4 by omitting node 3, we have \(c_{24} \leq c_{23} + c_{34}\). Similarly, when skipping nodes 4 and 3, \(c_{51} \leq c_{54} + c_{43} + c_{31}\).

Therefore, we have analyzed the approximation ratio of the double-tree algorithm.

Theorem 1. The double-tree algorithm for the metric traveling salesman problem is a 2-approximation algorithm.

4. Christofides' algorithm

The basic strategy of the double-tree algorithm is to construct an Eulerian tour whose total cost is at most \(\alpha , \mathrm{OPT}\), then shortcut it to get an \(\alpha\)-approximation solution. The same strategy can be carried out to yield a 3/2-approximation algorithm.

Christofides' algorithm Find a minimum spanning tree \(T\). Let \(O\) be the set of nodes with odd degree in \(T\). Find a minimum-cost perfect matching \(M\) on \(O\). Add the set of edges of \(M\) to \(T\). Find an Eulerian tour. Shortcut the Eulerian tour.

Figure 2 illustrates the algorithm on a simple five-city instance of TSP.

The algorithm starts again with the minimum spanning tree \(T\). The reason we cannot directly find an Eulerian tour is that its leaf nodes all have degrees of one. However, by the handshaking lemma , there is an even number of odd-degree nodes. If these nodes can be paired up, then it becomes an Eulerian graph and we can proceed as before.

Let \(O\) be the set of odd-degree nodes in \(T\). To pair them up, we want to find a collection of edges that contain each node in \(O\) exactly once. This is called a perfect matching in graph theory. Given a complete graph (on an even number of nodes) with edge costs, there is a polynomial-time algorithm to find the perfect matching of the minimum total cost, known as the blossom algorithm .

For the minimum spanning tree \(T\) in Figure 2a, \( O = \{1, 2, 3, 5\}\). The minimum-cost perfect matching \(M\) on the complete graph induced by \(O\) is shown in Figure 2b. Adding the edges of \(M\) to \(T\), the result is an Eulerian graph, since we have added a new edge incident to each odd-degree node in \(T\). The remaining steps are the same as in the double-tree algorithm.

We want to show that the Eulerian graph has total cost of at most 3/2 \(\mathrm{OPT}\). Since the total cost of the minimum spanning tree \(T\) is at most \(\mathrm{OPT}\), we only need to show that the perfect matching \(M\) has cost at most 1/2 \(\mathrm{OPT}\).

We start with the optimal tour on the entire set of cities, the cost of which is \(\mathrm{OPT}\) by definition. Figure 3a presents a simplified illustration of the optimal tour; the solid circles represent nodes in \(O\). By omitting the nodes that are not in \(O\) from the optimal tour, we get a tour on \(O\), as shown in Figure 3b. By the shortcutting argument again, the total cost of the tour on \(O\) is at most \(\mathrm{OPT}\). Next, color the edges yellow and green, alternating colors as the tour is traversed, as illustrated in Figure 3c. This partitions the edges into two sets: the yellow set and the green set; each is a perfect matching on \(O\). Since the total cost of the two matchings is at most \(\mathrm{OPT}\), the cheaper one has cost at most 1/2 \(\mathrm{OPT}\). In other words, there exists a perfect matching on \(O\) of cost at most 1/2 \(\mathrm{OPT}\). Therefore, the minimum-cost perfect matching must have cost not greater than 1/2 \(\mathrm{OPT}\). This completes the proof of the following theorem.

Theorem 2. Christofides' algorithm for the metric traveling salesman problem is a 3/2-approximation algorithm.

• Williamson, D. P., & Shmoys, D. B. (2011). The Design of Approximation Algorithms. Cambridge University Press.

Written on Feb 10, 2019.

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures
• Dynamic Programming or DP
• What is memoization? A Complete tutorial
• Dynamic Programming (DP) Tutorial with Problems
• Tabulation vs Memoization
• Optimal Substructure Property in Dynamic Programming | DP-2
• Overlapping Subproblems Property in Dynamic Programming | DP-1
• Steps for how to solve a Dynamic Programming Problem

Advanced Topics

• Bitmasking and Dynamic Programming | Set 1 (Count ways to assign unique cap to every person)
• Digit DP | Introduction
• Sum over Subsets | Dynamic Programming

Easy problems in Dynamic programming

• Count all combinations of coins to make a given value sum (Coin Change II)
• Subset Sum Problem
• Introduction and Dynamic Programming solution to compute nCr%p
• Cutting a Rod | DP-13
• Painting Fence Algorithm
• Longest Common Subsequence (LCS)
• Longest Increasing Subsequence (LIS)
• Longest subsequence such that difference between adjacents is one
• Maximum size square sub-matrix with all 1s
• Min Cost Path | DP-6
• Longest Common Substring (Space optimized DP solution)
• Count ways to reach the nth stair using step 1, 2 or 3
• Count Unique Paths in matrix
• Unique paths in a Grid with Obstacles

Medium problems on Dynamic programming

• 0/1 Knapsack Problem
• Printing Items in 0/1 Knapsack
• Unbounded Knapsack (Repetition of items allowed)
• Egg Dropping Puzzle | DP-11
• Word Break Problem | DP-32
• Vertex Cover Problem (Dynamic Programming Solution for Tree)
• Tile Stacking Problem
• Box Stacking Problem | DP-22
• Partition problem | DP-18

Travelling Salesman Problem using Dynamic Programming

• Longest Palindromic Subsequence (LPS)
• Longest Common Increasing Subsequence (LCS + LIS)
• Find all distinct subset (or subsequence) sums of an array
• Weighted Job Scheduling
• Count Derangements (Permutation such that no element appears in its original position)
• Minimum insertions to form a palindrome | DP-28
• Ways to arrange Balls such that adjacent balls are of different types

Hard problems on Dynamic programming

• Palindrome Partitioning
• Word Wrap Problem
• The Painter's Partition Problem
• Program for Bridge and Torch problem
• Matrix Chain Multiplication | DP-8
• Printing brackets in Matrix Chain Multiplication Problem
• Maximum sum rectangle in a 2D matrix | DP-27
• Maximum profit by buying and selling a share at most k times
• Minimum cost to sort strings using reversal operations of different costs
• Count of AP (Arithmetic Progression) Subsequences in an array
• Introduction to Dynamic Programming on Trees
• Maximum height of Tree when any Node can be considered as Root
• Longest repeating and non-overlapping substring
• Top 20 Dynamic Programming Interview Questions

Travelling Salesman Problem (TSP):  

Given a set of cities and the distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. Note the difference between Hamiltonian Cycle and TSP. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact, many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle. 

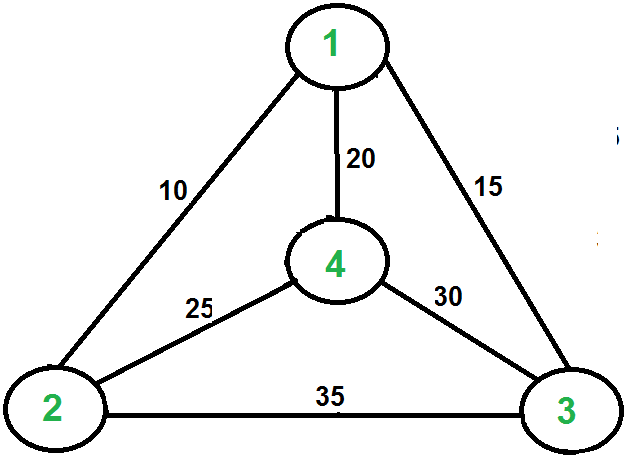
For example, consider the graph shown in the figure on the right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80. The problem is a famous NP-hard problem. There is no polynomial-time know solution for this problem. The following are different solutions for the traveling salesman problem. 

Naive Solution:  

1) Consider city 1 as the starting and ending point.

2) Generate all (n-1)! Permutations of cities. 

3) Calculate the cost of every permutation and keep track of the minimum cost permutation. 

4) Return the permutation with minimum cost. 

Time Complexity: ?(n!) 

Dynamic Programming:  

Let the given set of vertices be {1, 2, 3, 4,….n}. Let us consider 1 as starting and ending point of output. For every other vertex I (other than 1), we find the minimum cost path with 1 as the starting point, I as the ending point, and all vertices appearing exactly once. Let the cost of this path cost (i), and the cost of the corresponding Cycle would cost (i) + dist(i, 1) where dist(i, 1) is the distance from I to 1. Finally, we return the minimum of all [cost(i) + dist(i, 1)] values. This looks simple so far. 

Now the question is how to get cost(i)? To calculate the cost(i) using Dynamic Programming, we need to have some recursive relation in terms of sub-problems. 

Let us define a term C(S, i) be the cost of the minimum cost path visiting each vertex in set S exactly once, starting at 1 and ending at i . We start with all subsets of size 2 and calculate C(S, i) for all subsets where S is the subset, then we calculate C(S, i) for all subsets S of size 3 and so on. Note that 1 must be present in every subset.

Below is the dynamic programming solution for the problem using top down recursive+memoized approach:-

For maintaining the subsets we can use the bitmasks to represent the remaining nodes in our subset. Since bits are faster to operate and there are only few nodes in graph, bitmasks is better to use.

For example: –  

10100 represents node 2 and node 4 are left in set to be processed

010010 represents node 1 and 4 are left in subset.

NOTE:- ignore the 0th bit since our graph is 1-based

Time Complexity : O(n 2 *2 n ) where O(n* 2 n) are maximum number of unique subproblems/states and O(n) for transition (through for loop as in code) in every states.

Auxiliary Space: O(n*2 n ), where n is number of Nodes/Cities here.

For a set of size n, we consider n-2 subsets each of size n-1 such that all subsets don’t have nth in them. Using the above recurrence relation, we can write a dynamic programming-based solution. There are at most O(n*2 n ) subproblems, and each one takes linear time to solve. The total running time is therefore O(n 2 *2 n ). The time complexity is much less than O(n!) but still exponential. The space required is also exponential. So this approach is also infeasible even for a slightly higher number of vertices. We will soon be discussing approximate algorithms for the traveling salesman problem.

Next Article: Traveling Salesman Problem | Set 2  

References:  

http://www.lsi.upc.edu/~mjserna/docencia/algofib/P07/dynprog.pdf  

http://www.cs.berkeley.edu/~vazirani/algorithms/chap6.pdf  

Please Login to comment...

Similar reads.

• Dynamic Programming

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

traveling_salesman_problem #

Find the shortest path in G connecting specified nodes

This function allows approximate solution to the traveling salesman problem on networks that are not complete graphs and/or where the salesman does not need to visit all nodes.

This function proceeds in two steps. First, it creates a complete graph using the all-pairs shortest_paths between nodes in nodes . Edge weights in the new graph are the lengths of the paths between each pair of nodes in the original graph. Second, an algorithm (default: christofides for undirected and asadpour_atsp for directed) is used to approximate the minimal Hamiltonian cycle on this new graph. The available algorithms are:

christofides greedy_tsp simulated_annealing_tsp threshold_accepting_tsp asadpour_atsp

Once the Hamiltonian Cycle is found, this function post-processes to accommodate the structure of the original graph. If cycle is False , the biggest weight edge is removed to make a Hamiltonian path. Then each edge on the new complete graph used for that analysis is replaced by the shortest_path between those nodes on the original graph. If the input graph G includes edges with weights that do not adhere to the triangle inequality, such as when G is not a complete graph (i.e length of non-existent edges is infinity), then the returned path may contain some repeating nodes (other than the starting node).

A possibly weighted graph

collection (list, set, etc.) of nodes to visit

Edge data key corresponding to the edge weight. If any edge does not have this attribute the weight is set to 1.

Indicates whether a cycle should be returned, or a path. Note: the cycle is the approximate minimal cycle. The path simply removes the biggest edge in that cycle.

A function that returns a cycle on all nodes and approximates the solution to the traveling salesman problem on a complete graph. The returned cycle is then used to find a corresponding solution on G . method should be callable; take inputs G , and weight ; and return a list of nodes along the cycle.

Provided options include christofides() , greedy_tsp() , simulated_annealing_tsp() and threshold_accepting_tsp() .

If method is None : use christofides() for undirected G and asadpour_atsp() for directed G .

Other keyword arguments to be passed to the method function passed in.

List of nodes in G along a path with an approximation of the minimal path through nodes .

If G is a directed graph it has to be strongly connected or the complete version cannot be generated.

While no longer required, you can still build (curry) your own function to provide parameter values to the methods.

Otherwise, pass other keyword arguments directly into the tsp function.

An Approximation Algorithm for the Clustered Path Travelling Salesman Problem

• Conference paper
• First Online: 18 September 2022
• Cite this conference paper

• Jiaxuan Zhang 9 ,
• Suogang Gao 9 ,
• Bo Hou 9 &
• Wen Liu 9  

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 13513))

Included in the following conference series:

• International Conference on Algorithmic Applications in Management

487 Accesses

In this paper, we consider the clustered path travelling salesman problem. In this problem, we are given a complete graph \(G=(V,E)\) with edge weight satisfying the triangle inequality. In addition, the vertex set V is partitioned into clusters \(V_1,\cdots ,V_k\) . The objective of the problem is to find a minimum Hamiltonian path in G , and in the path all vertices of each cluster are visited consecutively. We provide a polynomial-time approximation algorithm for the problem.

Supported by the NSF of China (No. 11971146), the NSF of Hebei Province of China (No. A2019205089, No. A2019205092), Overseas Expertise Introduction Program of Hebei Auspices (25305008) and the Graduate Innovation Grant Program of Hebei Normal University (No. CXZZSS2022052).

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

An, H.-C., Kleinberg, R., Shmoys, D.B.: Improving Christofide’ algorithm for the s-t path TSP. J. ACM 62 (5), 1–28 (2015)

Article   MathSciNet   Google Scholar  

Anily, S., Bramel, J., Hertz, A.: A 5/3-approximation algorithm for the clustered traveling salesman tour and path problems. Oper. Res. Lett. 24 , 29–35 (1999)

Arkin, E.M., Hassin, R., Klein, L.: Restricted delivery problems on a network. Networks 29 , 205–216 (1994)

Bland, R.G., Shallcross, D.F.: Large travelling salesman problems arising from experiments in X-ray crystallography: a preliminary report on computation. Oper. Res. Lett. 8 (3), 125–128 (1989)

Chisman, J.A.: The clustered traveling salesman problem. Comput. Oper. Res. 2 , 115–119 (1975)

Article   Google Scholar  

Christofides, N.: Worst-case analysis of a new heuristic for the Travelling Salesman Problem. Technical report 388, Graduate School of Industrial Administration, Carnegie Mellon University (1976)

Google Scholar  

Diestel, R.: Graph Theory. Springer, New York (2017). https://doi.org/10.1007/978-3-662-53622-3

Book   MATH   Google Scholar  

Edmonds, J.: Paths, trees and flowers. Can. J. Math. 17 , 449–467 (1965)

Gendreau, M., Hertz, A., Laporte, G.: The traveling salesman problem with backhauls. Comput. Oper. Res. 23 , 501–508 (1996)

Grinman, A.: The Hungarian algorithm for weighted bipartite graphs. Seminar in Theoretical Computer Science (2015)

Grötschel, M., Holland, O.: Solution of large-scale symmetric traveling salesman problems. Math. Program. 51 , 141–202 (1991)

Gottschalk, C., Vygen, J.: Better s-t-tours by Gao trees. Math. Program. 172 , 191–207 (2018)

Guttmann-Beck, N., Hassin, R., Khuller, S., Raghavachari, B.: Approximation algorithms with bounded performance guarantees for the clustered traveling salesman problem. Algorithmica 28 , 422–437 (2000)

Hong, Y.M., Lai, H.J., Liu, Q.H.: Supereulerian digraphs. Discrete Math. 330 , 87–95 (2014)

Hoogeveen, J.A.: Analysis of Christofides’ heuristic: some paths are more difficult than cycles. Oper. Res. Lett. 10 , 291–295 (1991)

Jongens, K., Volgenant, T.: The symmetric clustered traveling salesman problem. Eur. J. Oper. Res. 19 , 68–75 (1985)

Kawasaki, M., Takazawa, T.: Improving approximation ratios for the clustered travelling salesman problem. J. Oper. Res. Soc. Jpn. 63 (2), 60–70 (2020)

MATH   Google Scholar  

Plante, R.D., Lowe, T.J., Chandrasekaran, R.: The product matrix travelling salesman problem: an application and solution heuristics. Oper. Res. 35 , 772–783 (1987)

Sebő, A., van Zuylen, A.: The salesman’s improved paths: a 3/2+1/34 approximation. In: Proceedings of 57th Annual IEEE Symposium on Foundations of Computer Science (FOCS), pp. 118–127 (2016)

Traub, V., Vygen, J.: Approaching 3/2 for the s-t path TSP. J. ACM 66 (2), 1–17 (2019)

Yao, A.: An O \((\left|E\right|\log \log \left|V\right|)\) algorithm for finding minimum spanning trees. Inf. Process. Lett. 4 , 21–23 (1975)

Zenklusen, R.: A 1.5-approximation for path TSP. In: Proceedings of the 30th Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 1539–1549 (2019)

Download references

Author information

Authors and affiliations.

Hebei Key Laboratory of Computational Mathematics and Applications, School of Mathematical Sciences, Hebei Normal University, Shijiazhuang, 050024, People’s Republic of China

Jiaxuan Zhang, Suogang Gao, Bo Hou & Wen Liu

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Wen Liu .

Editor information

Editors and affiliations.

Guangdong University of Technology, Guangzhou, China

University of Texas at Dallas, Richardson, TX, USA

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Cite this paper.

Zhang, J., Gao, S., Hou, B., Liu, W. (2022). An Approximation Algorithm for the Clustered Path Travelling Salesman Problem. In: Ni, Q., Wu, W. (eds) Algorithmic Aspects in Information and Management. AAIM 2022. Lecture Notes in Computer Science, vol 13513. Springer, Cham. https://doi.org/10.1007/978-3-031-16081-3_2

Download citation

DOI : https://doi.org/10.1007/978-3-031-16081-3_2

Published : 18 September 2022

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-16080-6

Online ISBN : 978-3-031-16081-3

eBook Packages : Computer Science Computer Science (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research