travel problems algebra

• Get started with computers
• Learn Microsoft Office
• Apply for a job
• Improve my work skills
• Design nice-looking docs
• Getting Started
• Smartphones & Tablets
• Typing Tutorial
• Online Learning
• Basic Internet Skills
• Online Safety
• Social Media
• Zoom Basics
• Google Docs
• Google Sheets
• Career Planning
• Resume Writing
• Cover Letters
• Job Search and Networking
• Business Communication
• Entrepreneurship 101
• Careers without College
• Job Hunt for Today
• 3D Printing
• Freelancing 101
• Personal Finance
• Sharing Economy
• Decision-Making
• Graphic Design
• Photography
• Image Editing
• Learning WordPress
• Language Learning
• Critical Thinking
• For Educators
• Translations
• Staff Picks
• English expand_more expand_less

Algebra Topics  - Distance Word Problems

Algebra topics  -, distance word problems, algebra topics distance word problems.

Algebra Topics: Distance Word Problems

Lesson 10: distance word problems.

/en/algebra-topics/introduction-to-word-problems/content/

What are distance word problems?

Distance word problems are a common type of algebra word problems. They involve a scenario in which you need to figure out how fast , how far , or how long one or more objects have traveled. These are often called train problems because one of the most famous types of distance problems involves finding out when two trains heading toward each other cross paths.

In this lesson, you'll learn how to solve train problems and a few other common types of distance problems. But first, let's look at some basic principles that apply to any distance problem.

The basics of distance problems

There are three basic aspects to movement and travel: distance , rate , and time . To understand the difference among these, think about the last time you drove somewhere.

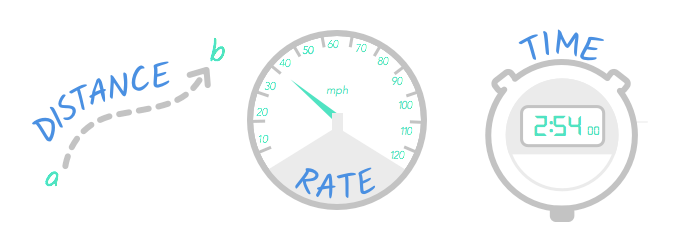
The distance is how far you traveled. The rate is how fast you traveled. The time is how long the trip took.

The relationship among these things can be described by this formula:

distance = rate x time d = rt

In other words, the distance you drove is equal to the rate at which you drove times the amount of time you drove. For an example of how this would work in real life, just imagine your last trip was like this:

• You drove 25 miles—that's the distance .
• You drove an average of 50 mph—that's the rate .
• The drive took you 30 minutes, or 0 .5 hours—that's the time .

According to the formula, if we multiply the rate and time , the product should be our distance.

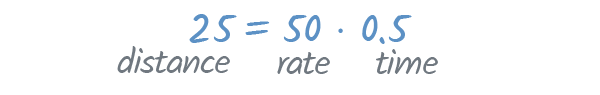
And it is! We drove 50 mph for 0.5 hours—and 50 ⋅ 0.5 equals 25 , which is our distance.

What if we drove 60 mph instead of 50? How far could we drive in 30 minutes? We could use the same formula to figure this out.

60 ⋅ 0.5 is 30, so our distance would be 30 miles.

Solving distance problems

When you solve any distance problem, you'll have to do what we just did—use the formula to find distance , rate , or time . Let's try another simple problem.

On his day off, Lee took a trip to the zoo. He drove an average speed of 65 mph, and it took him two-and-a-half hours to get from his house to the zoo. How far is the zoo from his house?

First, we should identify the information we know. Remember, we're looking for any information about distance, rate, or time. According to the problem:

• The rate is 65 mph.
• The time is two-and-a-half hours, or 2.5 hours.
• The distance is unknown—it's what we're trying to find.

You could picture Lee's trip with a diagram like this:

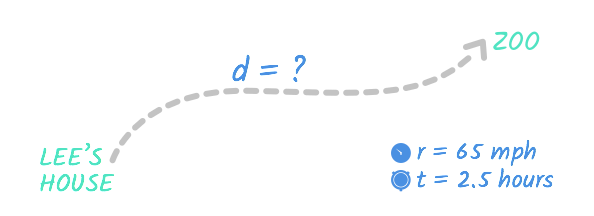
This diagram is a start to understanding this problem, but we still have to figure out what to do with the numbers for distance , rate , and time . To keep track of the information in the problem, we'll set up a table. (This might seem excessive now, but it's a good habit for even simple problems and can make solving complicated problems much easier.) Here's what our table looks like:

We can put this information into our formula: distance = rate ⋅ time .

We can use the distance = rate ⋅ time formula to find the distance Lee traveled.

The formula d = rt looks like this when we plug in the numbers from the problem. The unknown distance is represented with the variable d .

d = 65 ⋅ 2.5

To find d , all we have to do is multiply 65 and 2.5. 65 ⋅ 2.5 equals 162.5 .

We have an answer to our problem: d = 162.5. In other words, the distance Lee drove from his house to the zoo is 162.5 miles.

Be careful to use the same units of measurement for rate and time. It's possible to multiply 65 miles per hour by 2.5 hours because they use the same unit: an hour . However, what if the time had been written in a different unit, like in minutes ? In that case, you'd have to convert the time into hours so it would use the same unit as the rate.

Solving for rate and time

In the problem we just solved we calculated for distance , but you can use the d = rt formula to solve for rate and time too. For example, take a look at this problem:

After work, Janae walked in her neighborhood for a half hour. She walked a mile-and-a-half total. What was her average speed in miles per hour?

We can picture Janae's walk as something like this:

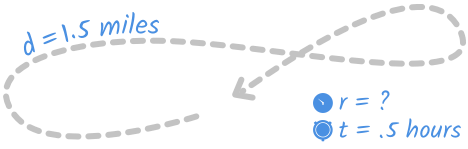
And we can set up the information from the problem we know like this:

The table is repeating the facts we already know from the problem. Janae walked one-and-a-half miles or 1.5 miles in a half hour, or 0.5 hours.

As always, we start with our formula. Next, we'll fill in the formula with the information from our table.

The rate is represented by r because we don't yet know how fast Janae was walking. Since we're solving for r , we'll have to get it alone on one side of the equation.

1.5 = r ⋅ 0.5

Our equation calls for r to be multiplied by 0.5, so we can get r alone on one side of the equation by dividing both sides by 0.5: 1.5 / 0.5 = 3 .

r = 3 , so 3 is the answer to our problem. Janae walked 3 miles per hour.

In the problems on this page, we solved for distance and rate of travel, but you can also use the travel equation to solve for time . You can even use it to solve certain problems where you're trying to figure out the distance, rate, or time of two or more moving objects. We'll look at problems like this on the next few pages.

Two-part and round-trip problems

Do you know how to solve this problem?

Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph, then he drove on the interstate at an average of 70 mph. The trip took three-and-a-half hours total. How far did Bill drive on the interstate?

This problem is a classic two-part trip problem because it's asking you to find information about one part of a two-part trip. This problem might seem complicated, but don't be intimidated!

You can solve it using the same tools we used to solve the simpler problems on the first page:

• The travel equation d = rt
• A table to keep track of important information

Let's start with the table . Take another look at the problem. This time, the information relating to distance , rate , and time has been underlined.

Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph , then he drove on the interstate at an average of 70 mph . The trip took three-and-a-half hours total. How far did Bill drive on the interstate?

If you tried to fill in the table the way we did on the last page, you might have noticed a problem: There's too much information. For instance, the problem contains two rates— 30 mph and 70 mph . To include all of this information, let's create a table with an extra row. The top row of numbers and variables will be labeled in town , and the bottom row will be labeled interstate .

We filled in the rates, but what about the distance and time ? If you look back at the problem, you'll see that these are the total figures, meaning they include both the time in town and on the interstate. So the total distance is 225 . This means this is true:

Interstate distance + in-town distance = Total distance

Together, the interstate distance and in-town distance are equal to the total distance. See?

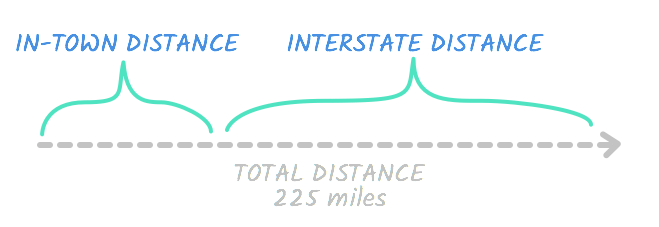
In any case, we're trying to find out how far Bill drove on the interstate , so let's represent this number with d . If the interstate distance is d , it means the in-town distance is a number that equals the total, 225 , when added to d . In other words, it's equal to 225 - d .

We can fill in our chart like this:

We can use the same technique to fill in the time column. The total time is 3.5 hours . If we say the time on the interstate is t , then the remaining time in town is equal to 3.5 - t . We can fill in the rest of our chart.

Now we can work on solving the problem. The main difference between the problems on the first page and this problem is that this problem involves two equations. Here's the one for in-town travel :

225 - d = 30 ⋅ (3.5 - t)

And here's the one for interstate travel :

If you tried to solve either of these on its own, you might have found it impossible: since each equation contains two unknown variables, they can't be solved on their own. Try for yourself. If you work either equation on its own, you won't be able to find a numerical value for d . In order to find the value of d , we'll also have to know the value of t .

We can find the value of t in both problems by combining them. Let's take another look at our travel equation for interstate travel.

While we don't know the numerical value of d , this equation does tell us that d is equal to 70 t .

Since 70 t and d are equal , we can replace d with 70 t . Substituting 70 t for d in our equation for interstate travel won't help us find the value of t —all it tells us is that 70 t is equal to itself, which we already knew.

But what about our other equation, the one for in-town travel?

When we replace the d in that equation with 70 t , the equation suddenly gets much easier to solve.

225 - 70t = 30 ⋅ (3.5 - t)

Our new equation might look more complicated, but it's actually something we can solve. This is because it only has one variable: t . Once we find t , we can use it to calculate the value of d —and find the answer to our problem.

To simplify this equation and find the value of t , we'll have to get the t alone on one side of the equals sign. We'll also have to simplify the right side as much as possible.

Let's start with the right side: 30 times (3.5 - t ) is 105 - 30 t .

225 - 70t = 105 - 30t

Next, let's cancel out the 225 next to 70 t . To do this, we'll subtract 225 from both sides. On the right side, it means subtracting 225 from 105 . 105 - 225 is -120 .

- 70t = -120 - 30t

Our next step is to group like terms—remember, our eventual goal is to have t on the left side of the equals sign and a number on the right . We'll cancel out the -30 t on the right side by adding 30 t to both sides. On the right side, we'll add it to -70 t . -70 t + 30 t is -40 t .

- 40t = -120

Finally, to get t on its own, we'll divide each side by its coefficient: -40. -120 / - 40 is 3 .

So t is equal to 3 . In other words, the time Bill traveled on the interstate is equal to 3 hours . Remember, we're ultimately trying to find the distanc e Bill traveled on the interstate. Let's look at the interstate row of our chart again and see if we have enough information to find out.

It looks like we do. Now that we're only missing one variable, we should be able to find its value pretty quickly.

To find the distance, we'll use the travel formula distance = rate ⋅ time .

We now know that Bill traveled on the interstate for 3 hours at 70 mph , so we can fill in this information.

d = 3 ⋅ 70

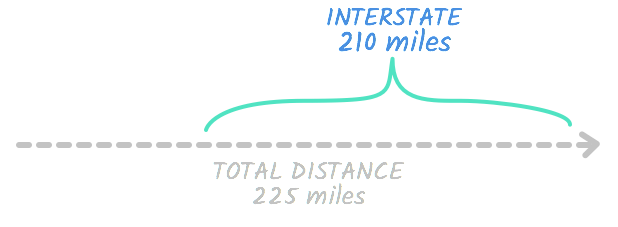
Finally, we finished simplifying the right side of the equation. 3 ⋅ 70 is 210 .

So d = 210 . We have the answer to our problem! The distance is 210 . In other words, Bill drove 210 miles on the interstate.

Solving a round-trip problem

It might have seemed like it took a long time to solve the first problem. The more practice you get with these problems, the quicker they'll go. Let's try a similar problem. This one is called a round-trip problem because it describes a round trip—a trip that includes a return journey. Even though the trip described in this problem is slightly different from the one in our first problem, you should be able to solve it the same way. Let's take a look:

Eva drove to work at an average speed of 36 mph. On the way home, she hit traffic and only drove an average of 27 mph. Her total time in the car was 1 hour and 45 minutes, or 1.75 hours. How far does Eva live from work?

If you're having trouble understanding this problem, you might want to visualize Eva's commute like this:

As always, let's start by filling in a table with the important information. We'll make a row with information about her trip to work and from work .

1.75 - t to describe the trip from work. (Remember, the total travel time is 1.75 hours , so the time to work and from work should equal 1.75 .)

From our table, we can write two equations:

• The trip to work can be represented as d = 36 t .
• The trip from work can be represented as d = 27 (1.75 - t ) .

In both equations, d represents the total distance. From the diagram, you can see that these two equations are equal to each other—after all, Eva drives the same distance to and from work .

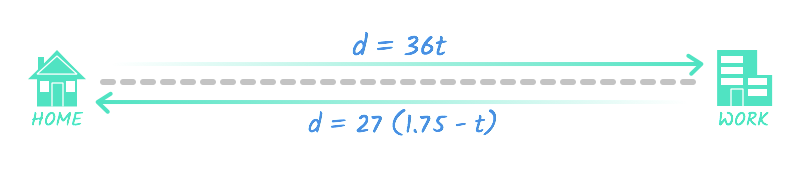
Just like with the last problem we solved, we can solve this one by combining the two equations.

We'll start with our equation for the trip from work .

d = 27 (1.75 - t)

Next, we'll substitute in the value of d from our to work equation, d = 36 t . Since the value of d is 36 t , we can replace any occurrence of d with 36 t .

36t = 27 (1.75 - t)

Now, let's simplify the right side. 27 ⋅(1.75 - t ) is 47.25 .

36t = 47.25 - 27t

Next, we'll cancel out -27 t by adding 27 t to both sides of the equation. 36 t + 27 t is 63 t .

63t = 47.25

Finally, we can get t on its own by dividing both sides by its coefficient: 63 . 47.25 / 63 is .75 .

t is equal to .75 . In other words, the time it took Eva to drive to work is .75 hours . Now that we know the value of t , we'll be able to can find the distance to Eva's work.

If you guessed that we were going to use the travel equation again, you were right. We now know the value of two out of the three variables, which means we know enough to solve our problem.

First, let's fill in the values we know. We'll work with the numbers for the trip to work . We already knew the rate : 36 . And we just learned the time : .75 .

d = 36 ⋅ .75

Now all we have to do is simplify the equation: 36 ⋅ .75 = 27 .

d is equal to 27 . In other words, the distance to Eva's work is 27 miles . Our problem is solved.

Intersecting distance problems

An intersecting distance problem is one where two things are moving toward each other. Here's a typical problem:

Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading to Springfield at the same time a train leaves Springfield heading to Pawnee. One train is moving at a speed of 45 mph, and the other is moving 60 mph. How long will they travel before they meet?

This problem is asking you to calculate how long it will take these two trains moving toward each other to cross paths. This might seem confusing at first. Even though it's a real-world situation, it can be difficult to imagine distance and motion abstractly. This diagram might help you get a sense of what this situation looks like:

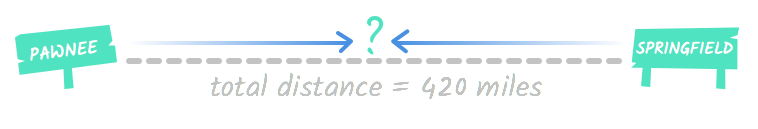
If you're still confused, don't worry! You can solve this problem the same way you solved the two-part problems on the last page. You'll just need a chart and the travel formula .

Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading toward Springfield at the same time a train leaves Springfield heading toward Pawnee. One train is moving at a speed of 45 mph , and the other is moving 60 mph . How long will they travel before they meet?

Let's start by filling in our chart. Here's the problem again, this time with the important information underlined. We can start by filling in the most obvious information: rate . The problem gives us the speed of each train. We'll label them fast train and slow train . The fast train goes 60 mph . The slow train goes only 45 mph .

We can also put this information into a table:

We don't know the distance each train travels to meet the other yet—we just know the total distance. In order to meet, the trains will cover a combined distance equal to the total distance. As you can see in this diagram, this is true no matter how far each train travels.

This means that—just like last time—we'll represent the distance of one with d and the distance of the other with the total minus d. So the distance for the fast train will be d , and the distance for the slow train will be 420 - d .

Because we're looking for the time both trains travel before they meet, the time will be the same for both trains. We can represent it with t .

The table gives us two equations: d = 60 t and 420 - d = 45 t . Just like we did with the two-part problems, we can combine these two equations.

The equation for the fast train isn't solvable on its own, but it does tell us that d is equal to 60 t .

The other equation, which describes the slow train, can't be solved alone either. However, we can replace the d with its value from the first equation.

420 - d = 45t

Because we know that d is equal to 60 t , we can replace the d in this equation with 60 t . Now we have an equation we can solve.

420 - 60t = 45t

To solve this equation, we'll need to get t and its coefficients on one side of the equals sign and any other numbers on the other. We can start by canceling out the -60 t on the left by adding 60 t to both sides. 45 t + 60 t is 105 t .

Now we just need to get rid of the coefficient next to t . We can do this by dividing both sides by 105 . 420 / 105 is 4 .

t = 4 . In other words, the time it takes the trains to meet is 4 hours . Our problem is solved!

If you want to be sure of your answer, you can check it by using the distance equation with t equal to 4 . For our fast train, the equation would be d = 60 ⋅ 4 . 60 ⋅ 4 is 240 , so the distance our fast train traveled would be 240 miles. For our slow train, the equation would be d = 45 ⋅ 4 . 45 ⋅ 4 is 180 , so the distance traveled by the slow train is 180 miles . Remember how we said the distance the slow train and fast train travel should equal the total distance? 240 miles + 180 miles equals 420 miles , which is the total distance from our problem. Our answer is correct.

Practice problem 1

Here's another intersecting distance problem. It's similar to the one we just solved. See if you can solve it on your own. When you're finished, scroll down to see the answer and an explanation.

Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove an average of 70 mph. How long did they drive before they met up?

Problem 1 answer

Here's practice problem 1:

Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove 70 mph. How long did they drive before they met up?

Answer: 2 hours .

Let's solve this problem like we solved the others. First, try making the chart. It should look like this:

Here's how we filled in the chart:

• Distance: Together, Dani and Jon will have covered the total distance between them by the time they meet up. That's 270 . Jon's distance is represented by d , so Dani's distance is 270 - d .
• Rate: The problem tells us Dani and Jon's speeds. Dani drives 65 mph , and Jon drives 70 mph .
• Time: Because Jon and Dani drive the same amount of time before they meet up, both of their travel times are represented by t .

Now we have two equations. The equation for Jon's travel is d = 65 t . The equation for Dani's travel is 270 - d = 70 t . To solve this problem, we'll need to combine them.

The equation for Jon tells us that d is equal to 65 t . This means we can combine the two equations by replacing the d in Dani's equation with 65 t .

270 - 65t = 70t

Let's get t on one side of the equation and a number on the other. The first step to doing this is to get rid of -65 t on the left side. We'll cancel it out by adding 65 t to both sides: 70 t + 65 t is 135 t .

All that's left to do is to get rid of the 135 next to the t . We can do this by dividing both sides by 135 : 270 / 135 is 2 .

That's it. t is equal to 2 . We have the answer to our problem: Dani and Jon drove 2 hours before they met up.

Overtaking distance problems

The final type of distance problem we'll discuss in this lesson is a problem in which one moving object overtakes —or passes —another. Here's a typical overtaking problem:

The Hill family and the Platter family are going on a road trip. The Hills left 3 hours before the Platters, but the Platters drive an average of 15 mph faster. If it takes the Platter family 13 hours to catch up with the Hill family, how fast are the Hills driving?

You can picture the moment the Platter family left for the road trip a little like this:

The problem tells us that the Platter family will catch up with the Hill family in 13 hours and asks us to use this information to find the Hill family's rate . Like some of the other problems we've solved in this lesson, it might not seem like we have enough information to solve this problem—but we do. Let's start making our chart. The distance can be d for both the Hills and the Platters—when the Platters catch up with the Hills, both families will have driven the exact same distance.

Filling in the rate and time will require a little more thought. We don't know the rate for either family—remember, that's what we're trying to find out. However, we do know that the Platters drove 15 mph faster than the Hills. This means if the Hill family's rate is r , the Platter family's rate would be r + 15 .

Now all that's left is the time. We know it took the Platters 13 hours to catch up with the Hills. However, remember that the Hills left 3 hours earlier than the Platters—which means when the Platters caught up, they'd been driving 3 hours more than the Platters. 13 + 3 is 16 , so we know the Hills had been driving 16 hours by the time the Platters caught up with them.

Our chart gives us two equations. The Hill family's trip can be described by d = r ⋅ 16 . The equation for the Platter family's trip is d = ( r + 15) ⋅ 13 . Just like with our other problems, we can combine these equations by replacing a variable in one of them.

The Hill family equation already has the value of d equal to r ⋅ 16. So we'll replace the d in the Platter equation with r ⋅ 16 . This way, it will be an equation we can solve.

r ⋅ 16 = (r + 15) ⋅ 13

First, let's simplify the right side: r ⋅ 16 is 16 r .

16r = (r + 15) ⋅ 13

Next, we'll simplify the right side and multiply ( r + 15) by 13 .

16r = 13r + 195

We can get both r and their coefficients on the left side by subtracting 13 r from 16 r : 16 r - 13 r is 3 r .

Now all that's left to do is get rid of the 3 next to the r . To do this, we'll divide both sides by 3: 195 / 3 is 65 .

So there's our answer: r = 65. The Hill family drove an average of 65 mph .

You can solve any overtaking problem the same way we solved this one. Just remember to pay special attention when you're setting up your chart. Just like the Hill family did in this problem, the person or vehicle who started moving first will always have a greater travel time.

Practice problem 2

Try solving this problem. It's similar to the problem we just solved. When you're finished, scroll down to see the answer and an explanation.

A train moving 60 mph leaves the station at noon. An hour later, a train moving 80 mph leaves heading the same direction on a parallel track. What time does the second train catch up to the first?

Problem 2 answer

Here's practice problem 2:

Answer: 4 p.m.

To solve this problem, start by making a chart. Here's how it should look:

Here's an explanation of the chart:

• Distance: Both trains will have traveled the same distance by the time the fast train catches up with the slow one, so the distance for both is d .
• Rate: The problem tells us how fast each train was going. The fast train has a rate of 80 mph , and the slow train has a rate of 60 mph .
• Time: We'll use t to represent the fast train's travel time before it catches up. Because the slow train started an hour before the fast one, it will have been traveling one hour more by the time the fast train catches up. It's t + 1 .

Now we have two equations. The equation for the fast train is d = 80 t . The equation for the slow train is d = 60 ( t + 1) . To solve this problem, we'll need to combine the equations.

The equation for the fast train says d is equal to 80 t . This means we can combine the two equations by replacing the d in the slow train's equation with 80 t .

80t = 60 (t + 1)

First, let's simplify the right side of the equation: 60 ⋅ ( t + 1) is 60 t + 60 .

80t = 60t + 60

To solve the equation, we'll have to get t on one side of the equals sign and a number on the other. We can get rid of 60 t on the right side by subtracting 60 t from both sides: 80 t - 60 t is 20 t .

Finally, we can get rid of the 20 next to t by dividing both sides by 20 . 60 divided by 20 is 3 .

So t is equal to 3 . The fast train traveled for 3 hours . However, it's not the answer to our problem. Let's look at the original problem again. Pay attention to the last sentence, which is the question we're trying to answer.

Our problem doesn't ask how long either of the trains traveled. It asks what time the second train catches up with the first.

The problem tells us that the slow train left at noon and the fast one left an hour later. This means the fast train left at 1 p.m . From our equations, we know the fast train traveled 3 hours . 1 + 3 is 4 , so the fast train caught up with the slow one at 4 p.m . The answer to the problem is 4 p.m .

/en/algebra-topics/algebra-quiz/content/

Module 9: Multi-Step Linear Equations

Using the distance, rate, and time formula, learning outcomes.

• Use the problem-solving method to solve problems using the distance, rate, and time formula

One formula you’ll use often in algebra and in everyday life is the formula for distance traveled by an object moving at a constant speed. The basic idea is probably already familiar to you. Do you know what distance you traveled if you drove at a steady rate of [latex]60[/latex] miles per hour for [latex]2[/latex] hours? (This might happen if you use your car’s cruise control while driving on the Interstate.) If you said [latex]120[/latex] miles, you already know how to use this formula!

The math to calculate the distance might look like this:

[latex]\begin{array}{}\\ \text{distance}=\left(\Large\frac{60\text{ miles}}{1\text{ hour}}\normalsize\right)\left(2\text{ hours}\right)\hfill \\ \text{distance}=120\text{ miles}\hfill \end{array}[/latex]

In general, the formula relating distance, rate, and time is

[latex]\text{distance}\text{=}\text{rate}\cdot \text{time}[/latex]

Distance, Rate, and Time

For an object moving at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula

[latex]d=rt[/latex]

where [latex]d=[/latex] distance, [latex]r=[/latex] rate, and [latex]t=[/latex] time.

Notice that the units we used above for the rate were miles per hour, which we can write as a ratio [latex]\Large\frac{miles}{hour}[/latex]. Then when we multiplied by the time, in hours, the common units “hour” divided out. The answer was in miles.

Jamal rides his bike at a uniform rate of [latex]12[/latex] miles per hour for [latex]3\Large\frac{1}{2}[/latex] hours. How much distance has he traveled?

In the following video we provide another example of how to solve for distance given rate and time.

Rey is planning to drive from his house in San Diego to visit his grandmother in Sacramento, a distance of [latex]520[/latex] miles. If he can drive at a steady rate of [latex]65[/latex] miles per hour, how many hours will the trip take?

Show Solution

In the following video we show another example of how to find rate given distance and time.

• Question ID 145550, 145553,145619,145620. Authored by : Lumen Learning. License : CC BY: Attribution
• Ex: Find the Rate Given Distance and Time. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/3rYh32ErDaE . License : CC BY: Attribution
• Example: Solve a Problem using Distance = Rate x Time. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/lMO1L_CvH4Y . License : CC BY: Attribution
• Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Rate, Time, Distance - Algebra Word Problems

In these lessons, we will learn about rate, time, distance word problems and how to solve “motion” word problems.

Related Pages Rate, Time, Distance Word Problems Distance Problems Distance Word Problems Average Speed Problems

Motion Word Problems: Rate, Time, Distance

The following diagram shows how to solve Rate-Time-Distance Problems. Scroll down the page for more examples and solutions on how to solve Rate-Time-Distance Problems or Motion Problems.

Students learn to solve introductory “motion” word problems - for example, cars traveling in opposite directions, bikers traveling toward each other, or one plane overtaking another. Students should first draw a diagram to represent the relationship between the distances involved in the problem, then set up a chart based on the formula rate times time = distance. The chart is then used to set up the equation.

Example: Two cars leave from the same place at the same time and travel in opposite directions. One car travels at 55 mph and the other at 75 mph. After how many hours will they be 520 miles apart?

Algebra Word Problem: Distance Rate and Time Appropriate for a student in Algebra 1 or Algebra 2

Example: Two private jets start from Chicago and travel in opposite directions. The speed of the first jet is ten less than two times the speed of the second jet. In 3 hours they are 105 miles apart. Find the speed of each jet.

Algebra & Rate, Time, Distance Problems Examples:

• A passenger train travels ate 80 mph. A freight train travels at 30 mph. If they travel in opposite directions. How long will it take before they are 275 miles apart?
• Sue can ride her bike 12 miles per hour faster than Mary can walk. Sue rides 95 miles in the same time Mary walks 35 miles. What is each person’s rate?

Distance, Rate, Time Word Problems Examples: An object is in uniform motion when it moves without changing its speed, or rate. The examples illustrate three types of problems involving uniform motion. Each is solved by using a chart, a sketch, and the distance formula.

• Lea left home and drove toward the ferry office at an average speed of 22 km/h. Trevon left at the same time and drove in the opposite direction with an average speed of 43 km/h. How long does Trevon need to drive before they are 65 km apart?
• Maria left home and traveled toward the capital at the average speed of 80 km./h. Some time later Imani left traveling in the opposite direction with the average speed of 45 km/h. After Maria had traveled for six hours they were 705 km apart. Find the number of hours Imani traveled.
• A passenger train traveled to the repair yards and back. On the trip there it traveled 68 mph and on the return trip it went 85 mph. How long did the trio there take if the return trip took four hours?
• A submarine traveled to St. Vincent and back. It took three hours less time to get there than it did to get back. The average speed on the trip there was 30 km/h. The average speed on the way back was 20 km/h. How many hours did the trip there take?
• Micaela left the hardware store and traveled toward her friend’s house at an average speed of 25 km/h. Nicole left some them later traveling in the same direction at an average speed of 30 km/h. After traveling for five hours, Nicole caught up with Micaela. How long did Macaela travel before Nicole caught up?
• A passenger plane left New York and flew east. A jet left one hour later flying at 280 km/h in an effort to catch up to the passenger plane. After flying for seven hours, the jet finally caught up. Find the passenger plane’s average speed.

Challenge #1 Julio left school and drove toward the recycling plant at an average speed of 30 km/h. Aliyah left four hours later and drove in the opposite direction with an average speed of 50 km/h. Find the number of hours Aliyah needs to drive before they are 280 km apart.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

"Distance" Word Problems

Explanation More Examples

What is a "distance" word problem?

"Distance" word problems, often also called "uniform rate" problems, involve something travelling at some fixed and steady ("uniform") pace ("rate", "velocity", or "speed"), or else you are told to regard to object as moving at some average speed.

Content Continues Below

MathHelp.com

Distance Word Problems

Whenever you read a problem that involves "how fast", "how far", or "for how long", you should think of the distance equation, d = rt , where d stands for distance, r stands for the (constant or average) rate of speed, and t stands for time.

Make sure that the units for time and distance agree with the units for the rate. For instance, if they give you a rate of feet per second, then your time must be in seconds and your distance must be in feet. Sometimes they try to trick you by using mis-matched units, and you have to catch this and convert to the correct units.

In case you're wondering, this type of exercise requires that the rate be fixed and steady (that is, unchanging) for the d = rt formula to work. The only way you can deal with a speed that might be changing over time is to take the average speed over the time or distance in question. Working directly with changing speeds will be something you'll encounter in calculus, as it requires calculus-based (or more advanced) methods.

What is the difference between a fixed speed and an average speed?

A fixed-speed exercise is one in which the car, say, is always going exactly sixty miles an hour; in three hours, the car, on cruise-control, will have gone 180 miles. An average-speed exercise is one in which the car, say, averaged forty miles an hour, but this average includes the different speeds related to stop lights, highways, and back roads; in three hours the car went 120 miles, though the car's speed was not constant. Most of the exercises you'll see will be fixed-speed exercises, but obviously they're not very "real world". It's a simplification they do in order to make the situation feasible using only algebraic methods.

What is an example of a "distance" word problem?

• A 555 -mile, 5 -hour plane trip was flown at two speeds. For the first part of the trip, the average speed was 105 mph. Then the tailwind picked up, and the remainder of the trip was flown at an average speed of 115 mph. For how long did the plane fly at each speed?

There is a method for setting up and solving these exercises that I first encountered well after I'd actually been doing them while taking a class as an undergraduate. But, as soon as I was introduced to the method, I switched over, because it is *so* way easier.

First I set up a grid, with the columns being labelled with the variables from the "distance" formula, and the rows being labelled with the "parts" involved:

In the first part, the plane covered some distance. I don't know how much, so I'll need a variable to stand for this unknown value. I'll use the variable they give me in the distance equation:

They gave me the speed, or rate, for this part, so I'll add this to my table:

The plane flew for some amount of time during this first part, but I don't know how long that was. So I need a variable to stand for this unknown value; I'll use the variable from the distance equation:

For the second part, the plane travelled the rest of the total distance. I don't know the exact distance that was flown during this second part, but I do know that it was "however much was left of the 555 miles, after the first d miles were flown in the first part. "How much was left after [some amount] was taken out" is expressed with subtraction: I take the amount that has been taken care of already, and subtract this from whatever was the total. Adding this to my table, I get:

They've given me the speed, or rate, for the second part, and I can use the same "How much is left?" construction for whatever was the time for this second part. So now my table looks like this:

For the "total" row, I add down (or take info from the exercise statement):

Advertisement

Why did I not add down in the "rate" column? Because I cannot add rates! In this exercise, adding the rates would have said that the average rate for the entire trip was 105 + 115 = 220 miles per hour. But obviously this makes no sense.

The genius of this table-based method of set-up is that I can now create equations from the rows and columns. In this exercise, there is more than one way to proceed. I'll work with the "distance" equation to create expressions for the distances covered in each part.

Multiplying across, the first row tells me that the distance covered in the first part of the flight was:

1st part distance: 105 t

Again multiplying across, the second row tells me that the distance covered in the second part of the flight was:

2nd part distance: 115(5 − t )

I can add these two partial-distance expressions, and set them equal to the known total distance:

105 t + 115(5 − t ) = 555

This is an equation in one variable, which I can solve:

105 t + 115(5 − t ) = 555 105 t + 575 − 115 t = 555 575 − 10 t = 555 20 = 10 t 2 = t

Looking back at my table, I see the I had defined t to be the time that the plane spent in the air on the first part of its journey. Looking back at the original exercise, I see that they want to know the times that the plane spent at each of the two speeds.

I now have the time for the first part of the flight; the time was two hours. The exercise said that the entire trip was five hours, so the second part must have taken three hours (found by subtracting the first-part time from the total time). They haven't asked for the partial distances, so I now have all the information I need; no further computations are necessary. My answer is:

first part: 2 hours second part: 3 hours

When I was setting up my equation, I mentioned that there was more than one way to proceed. What was the other way? I could have used the table to create an expression for each of the two partial times, added, set the result equal to the given total, and solved for the variable d . Since the distance equation is d  =  rt , then the expressions for the partial times would be created by solving the equation for t  = . My work would have looked like this:

first part: d /105

second part: (555 − d )/115

adding: d /105 + (555 − d )/115 = 5 23 d + 11,655 − 21 d = 12,075 2 d = 420 d = 210

Looking back at my table, I would have seen that this gives me the distance covered in the first half of the flight. Looking back at the exercise, I would have seeing that they are wanting times, not distances. So I would have back-solved for the time for the first part, and then done the subtraction to find the time for the second part. My work would have had more steps, but my answer would have been the same.

There are three things that I hope you take from the above example:

• Using a table or grid to keep track of what you're doing can be incredibly helpful.
• It is important to clearly define your variables, so you know (by the end) what you'd meant (back in the beginning), so you can apply your results correctly.
• You should always check the original exercise, so you can be sure that you're answering the question that they'd actually asked.

(My value for the distance, found above, is correct, but was not what they'd asked for.) But even more important to understand is this:

NEVER TRY TO ADD RATES! Think about it: If you drive 20 mph on one street, and 40 mph on another street, does that mean you averaged 60 mph? Of course not.

Can I even average the rates? If I drove at 20 mph for one hour, and then drove 60 mph for two hours, then I would have travelled 140 miles in three hours, or a little under 47 mph. But 47 is not the average of 20 and 60 .

As you can see, the actual math involved in solving this type of exercise is often quite simple. It's the set-up that's the hard part. So what follows are some more examples, but with just the set-up displayed. Try your hand at solving, and click on the links to get pop-ups from which to check your equations and solutions.

• An executive drove from home at an average speed of 30 mph to an airport where a helicopter was waiting. The executive boarded the helicopter and flew to the corporate offices at an average speed of 60 mph. The entire distance was 150 miles; the entire trip took three hours. Find the distance from the airport to the corporate offices.

I will start in the usual way, by setting up my table:

I have labelled my rows so it's clear how they relate to the exercise. Now I need to fill in the rows. As before, I don't know the distance or the time for the part where the executive was driving, so I'll use variables for these unknowns, along with the given rate.

For the flying portion of the trip, I'll use the "how much is left" construction, along with the given rate, to fill in my second row. I'll also fill in the totals.

The first row gives me the equation d  = 30 t . The second row is messier, giving me the equation:

150 − d = 60(3 − t )

There are various ways I can go from here; I think I'll solve this second equation for the variable d , and then set the results equal to each other.

150 − d = 60(3 − t ) 150 − 60(3 − t ) = d

Setting equal these two expressions for d , I get:

30 t = 150 − 60(3 − t )

Solve for t ; interpret the value; state the final answer.

• A car and a bus set out at 2 p.m. from the same point, headed in the same direction. The average speed of the car is 30 mph slower than twice the speed of the bus. In two hours, the car is 20 miles ahead of the bus. Find the rate of the car.

Both vehicles travelled for the same amount of time.

The car's values are expressed in terms of the bus' values, so I'll use variables for the bus' unknowns, and then define the car in terms of the bus' variables. This gives me:

(As it turns out, I won't need the "total" row this time.) The car's row gives me:

d + 20 = 2(2 r − 30)

This is not terribly helpful. The second row gives me:

I'll use the second equation to simplify the first equation by substituting " 2 r " from the second equation in for the " d " in the first equation. Then I'll solve the equation for the value of " r ". Finally, I'll need to interpret this value within the context of the exercise, and then I'll state the final answer.

(Remember that the expression for the car's speed, from the table, was 2 r  − 30 , so all you need to do is find the numerical value of this expression. Just evaluate; don't try to solve — again — for the value of r .)

URL: https://www.purplemath.com/modules/distance.htm

Page 1 Page 2

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• Privacy / Cookies
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

Algebra: Speed and Distance Problems

• Speed and Distance Problems
• Whipping Word Problems
• Interest Problems
• Area and Volume Problems
• Mixture and Combination Problems

Have you ever heard of a word problem like this one? "Train A heads north at an average speed of 95 miles per hour, leaving its station at the precise moment as another train, Train B, departs a different station, heading south at an average speed of 110 miles per hour. If these trains are inadvertently placed on the same track and start exactly 1,300 miles apart, how long until they collide?"

If that problem sounds familiar, it's probably because you watch a lot of television (like me). Whenever TV shows talk about math, it's usually in the context of a main character trying but failing miserably to solve the classic "impossible train problem." I have no idea why that is, but time and time again, this problem is singled out as the reason people hate math so much.

Kelley's Cautions

Make sure that the units match in a travel problem. For instance, if the problem says you traveled at 70 miles per hour for 15 minutes , then r = 70 and t = 0.25. Since the speed is given in miles per hour , the time should be in hours also, and 15 minutes is equal to .25 hours. I got that decimal by dividing 15 minutes by the number of minutes in an hour: 15 „ 60 = 1 „ 4 = 0.25.

In fact, it's not so hard. This, like any distance and rate of travel problem, only requires one simple formula:

Distance traveled ( D ) is equal to your rate of speed ( r ) multiplied by the time ( t ) you traveled that speed. What makes most distance and rate problems tricky is that you usually have two things traveling at once, so you need to use the formula twice at the same time. In this problem, you'll use it once for Train A and once for Train B.

To keep things straight in your mind, you should use little descriptive subscripts. For example, use the formula D A = r A · t A for Train A's distance, speed, and time values and use the formula D B = r B · t B for Train B.

Critical Point

The little A 's in the formula D A = r A · t A don't affect the values D, r , and t . They're just little labels to ensure that you only plug values corresponding to Train A into that formula.

Example 4 : Train A heads north at an average speed of 95 miles per hour, leaving its station at the precise moment as another train, Train B, departs a different station, heading south at an average speed of 110 miles per hour. If these trains are inadvertently placed on the same track and start exactly 1,300 miles apart, how long until they collide?

Solution : Two trains means two distance formulas: D A = r A · t A and D B = r B · t B . Your first goal is to plug in any values you can determine from the problem. Since Train A travels 95 mph, r A = 95; similarly, r B = 110.

Notice that the problem also says that the trains leave at the same time. This means that their travel times match exactly. Therefore, instead of denoting their travel times as t A and t B (which suggests they are different), I will write them both as t (which suggests they are equal). At this point, your formulas look like this:

Even though you added the distances in this problem, you won't always do so€”it depends on how the problem is worded. In Problem 3, for example, you will not calculate a sum.

Here's the tricky step. The trains are heading toward one another on a track that's 1,300 miles long. Therefore, they must collide when, together, both trains have traveled a total of 1,300 miles. Of course, Train B is going to travel more of those 1,300 miles than Train A, since it's traveling faster, but that doesn't matter. You don't even have to figure out how far each train will go. All that matters is that when D A + D B = 1300, it's curtains. Luckily, you happen to know what D A and D B are (95 t and 110 t , respectively) so plug those into the equation and solve.

You've Got Problems

Problem 3: Dave rode his bike from home to a 7-11 at an average speed of 17 mph, and the trip took 1.25 hours. However, as he pulled up to the store, he rode over some glass, causing both tires to go flat. Because of this rotten luck, he had to push his bike back home at an average speed of 3 mph. How long did the trip home take?

• D A + D B = 1300
• 95 t + 110 t = 1300
• 205 t = 1300
• t ‰ˆ 6.341 hours

So, the trains will collide in approximately 6.341 hours.

Excerpted from The Complete Idiot's Guide to Algebra © 2004 by W. Michael Kelley. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books , a member of Penguin Group (USA) Inc.

You can purchase this book at Amazon.com and Barnes & Noble .

• Algebra: Interest Problems

Here are the facts and trivia that people are buzzing about.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 8: Rational Expressions

8.8 Rate Word Problems: Speed, Distance and Time

Distance, rate and time problems are a standard application of linear equations. When solving these problems, use the relationship rate (speed or velocity) times time equals distance .

[latex]r\cdot t=d[/latex]

For example, suppose a person were to travel 30 km/h for 4 h. To find the total distance, multiply rate times time or (30km/h)(4h) = 120 km.

The problems to be solved here will have a few more steps than described above. So to keep the information in the problem organized, use a table. An example of the basic structure of the table is below:

The third column, distance, will always be filled in by multiplying the rate and time columns together. If given a total distance of both persons or trips, put this information in the distance column. Now use this table to set up and solve the following examples.

Example 8.8.1

Joey and Natasha start from the same point and walk in opposite directions. Joey walks 2 km/h faster than Natasha. After 3 hours, they are 30 kilometres apart. How fast did each walk?

The distance travelled by both is 30 km. Therefore, the equation to be solved is:

[latex]\begin{array}{rrrrrrl} 3r&+&3(r&+&2)&=&30 \\ 3r&+&3r&+&6&=&30 \\ &&&-&6&&-6 \\ \hline &&&&\dfrac{6r}{6}&=&\dfrac{24}{6} \\ \\ &&&&r&=&4 \text{ km/h} \end{array}[/latex]

This means that Natasha walks at 4 km/h and Joey walks at 6 km/h.

Example 8.8.2

Nick and Chloe left their campsite by canoe and paddled downstream at an average speed of 12 km/h. They turned around and paddled back upstream at an average rate of 4 km/h. The total trip took 1 hour. After how much time did the campers turn around downstream?

The distance travelled downstream is the same distance that they travelled upstream. Therefore, the equation to be solved is:

[latex]\begin{array}{rrlll} 12(t)&=&4(1&-&t) \\ 12t&=&4&-&4t \\ +4t&&&+&4t \\ \hline \dfrac{16t}{16}&=&\dfrac{4}{16}&& \\ \\ t&=&0.25&& \end{array}[/latex]

This means the campers paddled downstream for 0.25 h and spent 0.75 h paddling back.

Example 8.8.3

Terry leaves his house riding a bike at 20 km/h. Sally leaves 6 h later on a scooter to catch up with him travelling at 80 km/h. How long will it take her to catch up with him?

The distance travelled by both is the same. Therefore, the equation to be solved is:

[latex]\begin{array}{rrrrr} 20(t)&=&80(t&-&6) \\ 20t&=&80t&-&480 \\ -80t&&-80t&& \\ \hline \dfrac{-60t}{-60}&=&\dfrac{-480}{-60}&& \\ \\ t&=&8&& \end{array}[/latex]

This means that Terry travels for 8 h and Sally only needs 2 h to catch up to him.

Example 8.8.4

On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took 2.5 h. For how long did the car travel 40 km/h?

[latex]\begin{array}{rrrrrrr} 55(t)&+&40(2.5&-&t)&=&130 \\ 55t&+&100&-&40t&=&130 \\ &-&100&&&&-100 \\ \hline &&&&\dfrac{15t}{15}&=&\dfrac{30}{15} \\ \\ &&&&t&=&2 \end{array}[/latex]

This means that the time spent travelling at 40 km/h was 0.5 h.

Distance, time and rate problems have a few variations that mix the unknowns between distance, rate and time. They generally involve solving a problem that uses the combined distance travelled to equal some distance or a problem in which the distances travelled by both parties is the same. These distance, rate and time problems will be revisited later on in this textbook where quadratic solutions are required to solve them.

For Questions 1 to 8, find the equations needed to solve the problems. Do not solve.

• A is 60 kilometres from B. An automobile at A starts for B at the rate of 20 km/h at the same time that an automobile at B starts for A at the rate of 25 km/h. How long will it be before the automobiles meet?
• Two automobiles are 276 kilometres apart and start to travel toward each other at the same time. They travel at rates differing by 5 km/h. If they meet after 6 h, find the rate of each.
• Two trains starting at the same station head in opposite directions. They travel at the rates of 25 and 40 km/h, respectively. If they start at the same time, how soon will they be 195 kilometres apart?
• Two bike messengers, Jerry and Susan, ride in opposite directions. If Jerry rides at the rate of 20 km/h, at what rate must Susan ride if they are 150 kilometres apart in 5 hours?
• A passenger and a freight train start toward each other at the same time from two points 300 kilometres apart. If the rate of the passenger train exceeds the rate of the freight train by 15 km/h, and they meet after 4 hours, what must the rate of each be?
• Two automobiles started travelling in opposite directions at the same time from the same point. Their rates were 25 and 35 km/h, respectively. After how many hours were they 180 kilometres apart?
• A man having ten hours at his disposal made an excursion by bike, riding out at the rate of 10 km/h and returning on foot at the rate of 3 km/h. Find the distance he rode.
• A man walks at the rate of 4 km/h. How far can he walk into the country and ride back on a trolley that travels at the rate of 20 km/h, if he must be back home 3 hours from the time he started?

Solve Questions 9 to 22.

• A boy rides away from home in an automobile at the rate of 28 km/h and walks back at the rate of 4 km/h. The round trip requires 2 hours. How far does he ride?
• A motorboat leaves a harbour and travels at an average speed of 15 km/h toward an island. The average speed on the return trip was 10 km/h. How far was the island from the harbour if the trip took a total of 5 hours?
• A family drove to a resort at an average speed of 30 km/h and later returned over the same road at an average speed of 50 km/h. Find the distance to the resort if the total driving time was 8 hours.
• As part of his flight training, a student pilot was required to fly to an airport and then return. The average speed to the airport was 90 km/h, and the average speed returning was 120 km/h. Find the distance between the two airports if the total flying time was 7 hours.
• Sam starts travelling at 4 km/h from a campsite 2 hours ahead of Sue, who travels 6 km/h in the same direction. How many hours will it take for Sue to catch up to Sam?
• A man travels 5 km/h. After travelling for 6 hours, another man starts at the same place as the first man did, following at the rate of 8 km/h. When will the second man overtake the first?
• A motorboat leaves a harbour and travels at an average speed of 8 km/h toward a small island. Two hours later, a cabin cruiser leaves the same harbour and travels at an average speed of 16 km/h toward the same island. How many hours after the cabin cruiser leaves will it be alongside the motorboat?
• A long distance runner started on a course, running at an average speed of 6 km/h. One hour later, a second runner began the same course at an average speed of 8 km/h. How long after the second runner started will they overtake the first runner?
• Two men are travelling in opposite directions at the rate of 20 and 30 km/h at the same time and from the same place. In how many hours will they be 300 kilometres apart?
• Two trains start at the same time from the same place and travel in opposite directions. If the rate of one is 6 km/h more than the rate of the other and they are 168 kilometres apart at the end of 4 hours, what is the rate of each?
• Two cyclists start from the same point and ride in opposite directions. One cyclist rides twice as fast as the other. In three hours, they are 72 kilometres apart. Find the rate of each cyclist.
• Two small planes start from the same point and fly in opposite directions. The first plane is flying 25 km/h slower than the second plane. In two hours, the planes are 430 kilometres apart. Find the rate of each plane.
• On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took a total of 2.5 hours. For how long did the car travel at 40 km/h?
• Running at an average rate of 8 m/s, a sprinter ran to the end of a track and then jogged back to the starting point at an average of 3 m/s. The sprinter took 55 s to run to the end of the track and jog back. Find the length of the track.

Answer Key 8.8

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.4: Word problems

• Last updated
• Save as PDF
• Page ID 45030

• Darlene Diaz
• Santiago Canyon College via ASCCC Open Educational Resources Initiative

Now, let’s apply the techniques from this chapter to some common word problems. Word problems can be tricky. The goal is becoming proficient in translating an English sentence into a mathematical sentence. In this section, we focus on word problems modeled by a linear equation and solve. We discuss geometry problems including perimeter and triangles, number, and distance problems.

Number Problems

Example \(\pageindex{1}\).

If \(28\) less than five times a number is \(232\), what is the number?

First, let \(n\) be the number. Now, translate the key words in the sentence: \[\underset{\color{blue}{5n-28}}{\color{blue}{\underbrace{\color{black}{...28\text{ less than }\underset{5n}{\underbrace{\text{five times a number}}}}}}}\underset{=}{\underbrace{\text{is}}}\underset{232}{\underbrace{232}}...\nonumber\]

Notice, after translating, we obtain the equation \[5n-28=232\nonumber\]

Let's solve: \[\begin{array}{rl}5n-8=232&\text{Isolate the variable term }5n \\ 5n-28+\color{blue}{28}\color{black}{}=232+\color{blue}{28}\color{black}{}&\text{Simplify} \\ 5n=260&\text{Multiply by the reciprocal of }5 \\ \color{blue}{\frac{1}{5}}\color{black}{}\cdot 5n=260\cdot\color{blue}{\frac{1}{5}}\color{black}{}&\text{Simplify} \\ n=52&\text{Solution}\end{array}\nonumber\]

Thus, the number is \(52\).

Example \(\PageIndex{2}\)

Fifteen more than three times a number is the same as ten less than six times the number. What is the number?

Notice, this sentence is a bit more challenging than Example \(\PageIndex{1}\) , but we still follow the method. Let \(n\) be the number.

\[\underset{\color{blue}{3n+15}}{\color{blue}{\underbrace{\color{black}{\text{Fifteen more than }\underset{3n}{\underbrace{\text{three times a number }}} }}}}\underset{=}{\underbrace{\text{ is the same as }}}\underset{\color{blue}{6n-10}}{\color{blue}{\underbrace{\color{black}{\text{ ten less than }\underset{6n}{\underbrace{\text{ six times the number}}}}}}}\nonumber\]

Notice, after translating, we obtain the equation \[3n+15=6n-10\nonumber\]

Let's solve: \[\begin{array}{rl}3n+15=6n-10&\text{Combine like terms} \\ 3n+15+\color{blue}{(-6n)}\color{black}{}=6n-10+\color{blue}{(-6n)}\color{black}{}&\text{Simplify} \\ -3n+15=-10&\text{Isolate the variable term} \\ -3n+15+\color{blue}{(-15)}\color{black}{}=-10+\color{blue}{(-15)}\color{black}{}&\text{Simplify} \\ -3n=-25&\text{Multiply by the reciprocal of }-3 \\ \color{blue}{-\frac{1}{3}}\color{black}{}\cdot -3n=-25\cdot\color{blue}{-\frac{1}{3}}\color{black}{}&\text{Simplify} \\ n=\frac{25}{3}&\text{Solution}\end{array}\nonumber\]

Thus, the number is \(\frac{25}{3}\).

Consecutive Integers

Another type of number problem involves consecutive integers .

Definition: Consecutive Integers

Consecutive integers are integers that come one after the other (such as \(3,\: 4,\: 5,\) or \(−3,\: −2,\: −1\)).

• If we are trying to find several consecutive integers , it important to identify the first integer and then assign names to the following integers. E.g., if \(x\) is the first integer, then \(x + 1\) will be the next, and \(x + 2\) will be the following, and so on.
• If we are trying to find several even or odd consecutive integers , it important to identify the first integer and then assign names to the following even or odd integers. E.g., if \(x\) is the first integer, then \(x + 2\) will be the next odd or even integer, and \(x + 4\) will be the following, and so on.

Example \(\PageIndex{3}\)

The sum of three consecutive positive integers is \(93\). What are the positive integers?

Since we want to obtain three consecutive positive integers, then we can assign each integer as the following: \[\begin{array}{rl}x&\text{is the first integer} \\ x+1&\text{is the second integer} \\ x+2&\text{is the third integer}\end{array}\nonumber\]

The sum of these three integers is given to be \(93\). Translating this into an equation, we get \[x+(x+1)+(x+2)=93\nonumber\]

Let’s solve this equation for \(x\). Then we can obtain the other two integers.

\[\begin{array}{rl}x+(x+1)+(x+2)=93&\text{Rewrite without the parenthesis} \\ x+x+1+x+2=93&\text{Combine like terms} \\ 3x+3=93&\text{Isolate the variable term} \\ 3x+3+\color{blue}{(-3)}\color{black}{}=93+\color{blue}{(-3)}\color{black}{}&\text{Simplify} \\ 3x=90&\text{Multiply by the reciprocal of }3 \\ \color{blue}{\frac{1}{3}}\color{black}{}\cdot 3x=90\cdot\color{blue}{\frac{1}{3}}\color{black}{}&\text{Simplify} \\ x=30&\text{First integer}\end{array}\nonumber\]

Since the first integer is \(30\), the next two integers would be \[\begin{array}{rl}30+1=31&\text{is the second even integer} \\ 30+2=32&\text{is the third even integer}\end{array}\nonumber\]

Thus, the integers are \(30,\: 31,\) and \(32\).

Example \(\PageIndex{4}\)

The sum of three consecutive even positive integers is \(246\). What are the numbers?

Since we want to obtain three consecutive even positive integers , then we can assign each integer as the following: \[\begin{array}{rl}x&\text{is the first odd integer} \\ x+2&\text{is the second odd integer} \\ x+4&\text{is the third odd integer}\end{array}\nonumber\]

The sum of these three even integers is given to be \(246\). Translating this into an equation, we get \[x+(x+2)+(x+4)=246\nonumber\]

\[\begin{array}{rl}x+(x+2)+(x+4)=246&\text{Rewrite without the parenthesis} \\ x+x+2+x+4=246&\text{Combine like terms} \\ 3x+6=246&\text{Isolate the variable term} \\ 3x+6+\color{blue}{(-6)}\color{black}{}=246+\color{blue}{(-6)}\color{black}{}&\text{Simplify} \\ 3x=240&\text{Multiply by the reciprocal of }3 \\ \color{blue}{\frac{1}{3}}\color{black}{}\cdot 3x=240\cdot\color{blue}{\frac{1}{3}}\color{black}{}&\text{Simplify} \\ x=80&\text{First integer}\end{array}\nonumber\]

Since the first integer is 80, the next two even integers would be \[\begin{array}{rl}80+2=82&\text{is the second even integer} \\ 80+4=32&\text{is the third even integer}\end{array}\nonumber\]

Thus, the integers are \(80,\: 82,\) and \(84\).

Example \(\PageIndex{5}\)

Find three consecutive odd positive integers so that the sum of twice the first integer, the second integer, and three times the third integer is \(152\).

Since we want to obtain three consecutive odd positive integers , then we can assign each integer as the following: \[\begin{array}{rl}x&\text{is the first odd integer} \\ x+2&\text{is the second integer} \\ x+4&\text{is the third odd integer}\end{array}\nonumber\]

The sum of twice the first integer, the second integer, and three times the third integer is given to be \(152\). Translating this into an equation, we get \[2\cdot x+(x+2)+3\cdot (x+4)=152\nonumber\]

\[\begin{array}{rl}2\cdot x+(x+2)+3\cdot (x+4)=152&\text{Rewrite without the parenthesis} \\ 2x+x+2+3x+12=152&\text{Combine like terms} \\ 6x+14=152&\text{Isolate the variable term} \\ 6x+14+\color{blue}{(-14)}\color{black}{}=152+\color{blue}{(-14)}\color{black}{}&\text{Simplify} \\ 6x=138&\text{Multiply by the reciprocal of }6 \\ \color{blue}{\frac{1}{6}}\color{black}{}\cdot 6x=138\cdot\color{blue}{\frac{1}{6}}\color{black}{}&\text{Simplify} \\ x=23&\text{First integer}\end{array}\nonumber\]

Since the first integer is \(23\), the next two odd integers would be \[\begin{array}{rl}23+2=25&\text{is the second odd integer} \\ 23+4=27&\text{is the third odd integer}\end{array}\nonumber\]

Thus, the integers are \(23,\: 25,\) and \(27\).

Perimeter Problems

Another problem from geometry involves perimeter or the distance around an object.

Definition: Perimeter of a Rectangle

The formula for the perimeter of a rectangle is given by \[P=2w+2\ell ,\nonumber\] where \(w\) is the width and \(ℓ\) is the length of the rectangle.

Example \(\PageIndex{6}\)

The perimeter of a rectangle is \(44\) cm. The length is \(5\) less than double the width. Find the dimensions.

Let \(w\) be the width of the rectangle. Then the length is \(2w − 5\). Since the perimeter is \(44\text{ cm}\), the we can use the perimeter formula to obtain the dimensions.

\[\begin{array}{rl}P=2w+2\ell &\text{Substitute in the width, length, and perimeter} \\ 44=2(w)+2(2w-5)&\text{Rewrite with no parenthesis} \\ 44=2w+4w-10&\text{Combine like terms} \\ 44=6w-10&\text{Isolate the variable term} \\ 54=6w&\text{Multiply by the reciprocal of }6 \\ 9=w&\text{Length of the rectangle}\end{array}\nonumber\]

Since the width is \(9\text{ cm}\), then the length is \((2(9) − 5) = 13\text{ cm}\).

Sum of Angles in a Triangle

Given a triangle, the sum of the three angles is \(180^{\circ}\). I.e., if the angles in a triangle are \(a^{\circ},\: b^{\circ},\) and \(c^{\circ}\), then \[a^{\circ}+b^{\circ}+c^{\circ}=180^{\circ}\nonumber\]

German mathematician Bernhart Thibaut in 1809 tried to prove that the angles of a triangle add to \(180\) without using Euclid’s parallel postulate (a point of much debate in math history). He created a proof, but it was later shown to have an error in the proof.

Example \(\PageIndex{7}\)

The second angle of a triangle is double the first. The third angle is \(40\) less than the first. Find the three angles.

Let \(x\) be the measure of the first angle. Then \[\begin{array}{rl}2x&\text{is the measure of the second angle} \\ x-40&\text{is the measure of the third angle}\end{array}\nonumber\]

Since the sum of these three angles is \(180^{\circ}\), then we can write the equation \[x+2x+(x-40)=180\nonumber\]

Let’s solve for the first angle \(x\):

\[\begin{array}{rl}x + 2x + (x − 40) = 180 &\text{Rewrite without parenthesis} \\ x + 2x + x − 40 = 180 &\text{Combine like terms} \\ 4x − 40 = 180 &\text{Isolate the variable term} \\ 4x=220&\text{Multiply by the reciprocal of }4 \\ x=55&\text{Measure of the first angle}\end{array}\nonumber\]

Since the measure of the first angle is \(55^{\circ}\), then the measures of the second and third angle are

\[\begin{array}{rl} 2(55)=110^{\circ}&\text{is the measure of the second angle} \\ 55-40=15^{\circ}&\text{is the measure of the third angle}\end{array}\nonumber\]

Uniform Motion Problems

Another common application of linear equations is uniform motion problems. When solving uniform motion problems, we use the relationship \(rt = d\) or \[\text{rate (speed)}\cdot\text{time}=\text{distance}\nonumber\]

For example, if a person were to travel \(30\) miles per hour (mph) for \(4\) hours, to find the total distance we would multiply rate and the time: \((30)(4) = 120\). Hence, this person traveled a distance of \(120\) miles. The problems we solve in this section are just a few more steps than described. To keep the information in the problem organized, we use tables.

Opposite Directions

Example \(\pageindex{8}\).

Two joggers start from opposite ends of an \(8\) mile course running towards each other. One jogger is running at a rate of \(4\) miles per hour, and the other is running at a rate of \(6\) miles per hour. After how long will the joggers meet?

First, we can make a table to organize the given information and then create an equation. Let \(t\) represent the length of time until the joggers meet.

Table \(\PageIndex{1}\)

Now we can set up the equation. If the total distance is \(8\) miles, then \[4t=6t+8,\nonumber\] i.e., the sum of Jogger 1’s distance and Jogger 2’s distance is \(8\) miles. Let’s solve.

\[\begin{array}{rl}4t+6t=8&\text{Combine like terms} \\ 10t=8&\text{Multiply by the reciprocal of }10 \\ t=\frac{4}{5}&\text{Hours until they meet}\end{array}\nonumber\]

It will be \(\frac{4}{5}\) hours (or \(48\) minutes) until they meet.

Example \(\PageIndex{9}\)

Bob and Fred start from the same point and walk in opposite directions. Bob walks \(2\) miles per hour faster than Fred. After \(3\) hours they are \(30\) miles apart. How fast did each walk?

First, we can make a table to organize the given information and then create an equation. Let \(r\) represent the rate of Fred.

Table \(\PageIndex{2}\)

Now we can set up the equation. If the total distance is \(30\) miles, then \[3(r+2)+3r=30,\nonumber\] i.e., the sum of Bob’s distance and Fred’s distance is \(30\) miles. Let’s solve.

\[\begin{array}{rl}3(r+2)+3r=30&\text{Distribute} \\ 3r+6+3r=30&\text{Combine like terms} \\ 6r+6=30&\text{Isolate the variable term} \\ 6r=24&\text{Multiply by the reciprocal of }6 \\ r=4&\text{Rate of Fred}\end{array}\nonumber\]

Since the rate of Fred is \(4\) mph, then Bob’s rate is \(6\) mph \((4 + 2 = 6)\).

Example \(\PageIndex{10}\)

Two campers left their campsite by canoe and paddled downstream at an average speed of \(12\) miles per hour. They turned around and paddled back upstream at an average rate of \(4\) miles per hour. The total trip took \(1\) hour. After how much time did the campers turn around downstream?

First, we can make a table to organize the given information and then create an equation. Let \(t\) represent the time it took to travel upstream.

Table \(\PageIndex{3}\)

Now we can set up the equation. If the upstream and downstream routes’ distances are the same, then \[4t=12(1-t)\nonumber\]

Let’s solve.

\[\begin{array}{rl}4t=12(1-t)&\text{Distribute} \\ 4t=12-12t&\text{Combine like terms} \\ 16t=12&\text{Multiply by the reciprocal of }16 \\ t=\frac{12}{16}&\text{Reduce} \\ t=\frac{3}{4}&\text{Time going upstream}\end{array}\nonumber\]

Since the time going upstream is \(\frac{3}{4}\) hours, then downstream’s time is \(\frac{1}{4}\) hours \(\left( 1 −\frac{3}{4} = \frac{1}{4}\right)\). Thus, the campers spent \(15\) minutes going downstream.

Example \(\PageIndex{11}\)

Mike leaves his house traveling \(2\) miles per hour. Joy leaves \(6\) hours later to catch up with him traveling \(8\) miles per hour. How long will it take her to catch up with him?

First, we can make a table to organize the given information and then create an equation. Let \(t\) represent the time Joy traveled.

Table \(\PageIndex{4}\)

Now we can set up the equation. If Joy catches up to Mike, then Mike and Joy would have traveled the same distance. Hence, giving the equation \[2(t+6)=8t,\nonumber\] i.e., Mike’s distance and Joy’s distance are the same. Let’s solve.

\[\begin{array}{rl}2(t+6)=8t&\text{Distribute} \\ 2t+12=8t&\text{Combine like terms} \\ 12=6t&\text{Multiply by the reciprocal of }6 \\ 2=t&\text{Time Joy traveled}\end{array}\nonumber\]

Since the time Joy traveled was \(2\) hours, then Mike traveled \(8\) hours \((2 + 6 = 8)\). Thus, it took \(2\) hours for Joy to catch up with Mike.

The \(10,000\)-meter race is the longest standard track event. Ten-thousand meters is approximately \(6.2\) miles. The current (at the time of printing) world record for this race is held by Ethiopian Kenenisa Bekele with a time of \(26\) minutes, \(17.53\) seconds. That is a rate of \(12.7\) miles per hour.

Example \(\PageIndex{12}\)

On a \(130\)-mile trip, a car traveled at an average speed of \(55\) mph and then reduced its speed to \(40\) mph for the remainder of the trip. The trip took \(2.5\) hours. For how long did the car travel \(40\) mph?

First, we can make a table to organize the given information and then create an equation. Let \(t\) represent the time the car traveled at the faster speed.

Table \(\PageIndex{5}\)

Now we can set up the equation. Since the total distance of the trip was \(130\) miles, then \[55t+40(2.5-t)=130,\nonumber\] i.e., the sum of the first part’s distance and the second part’s distance is \(130\) miles. Let’s solve.

\[\begin{array}{rl} 55t + 40(2.5 − t) = 130 &\text{Distribute} \\ 55t + 100 − 40t = 130 &\text{Combine like terms} \\ 15t+100=130&\text{Isolate the variable term} \\ 15t=30&\text{Multiply by the reciprocal of }15 \\ t=2&\text{First part's travel time}\end{array}\nonumber\]

Since the first part of the trip took \(2\) hours, then the car traveled \(0.5\) hours (or \(30\) minutes) at \(40\) mph.

Word Problems Homework

Exercise \(\pageindex{1}\).

When five is added to three more than a certain number, the result is \(19\). What is the number?

Exercise \(\PageIndex{2}\)

If five is subtracted from three times a certain number, the result is \(10\). What is the number?

Exercise \(\PageIndex{3}\)

When \(18\) is subtracted from six times a certain number, the result is \(−42\). What is the number?

Exercise \(\PageIndex{4}\)

A certain number added twice to itself equals \(96\). What is the number?

Exercise \(\PageIndex{5}\)

A number plus itself, plus twice itself, plus \(4\) times itself, is equal to \(−104\). What is the number?

Exercise \(\PageIndex{6}\)

Sixty more than nine times a number is the same as two less than ten times the number. What is the number?

Exercise \(\PageIndex{7}\)

Eleven less than seven times a number is five more than six times the number. Find the number.

Exercise \(\PageIndex{8}\)

Fourteen less than eight times a number is three more than four times the number. What is the number?

Exercise \(\PageIndex{9}\)

The sum of three consecutive integers is \(108\). What are the integers?

Exercise \(\PageIndex{10}\)

The sum of three consecutive integers is \(−126\). What are the integers?

Exercise \(\PageIndex{11}\)

Find three consecutive integers such that the sum of the first, twice the second, and three times the third is \(−76\).

Exercise \(\PageIndex{12}\)

The sum of two consecutive even integers is \(106\). What are the integers?

Exercise \(\PageIndex{13}\)

The sum of three consecutive odd integers is \(189\). What are the integers?

Exercise \(\PageIndex{14}\)

The sum of three consecutive odd integers is \(255\). What are the integers?

Exercise \(\PageIndex{15}\)

Find three consecutive odd integers such that the sum of the first, two times the second, and three times the third is \(70\).

Exercise \(\PageIndex{16}\)

The second angle of a triangle is the same size as the first angle. The third angle is \(12\) degrees larger than the first angle. How large are the angles?

Exercise \(\PageIndex{17}\)

Two angles of a triangle are the same size. The third angle is \(12\) degrees smaller than the first angle. Find the measure the angles.

Exercise \(\PageIndex{18}\)

Two angles of a triangle are the same size. The third angle is \(3\) times as large as the first. How large are the angles?

Exercise \(\PageIndex{19}\)

The third angle of a triangle is the same size as the first. The second angle is \(4\) times the third. Find the measure of the angles.

Exercise \(\PageIndex{20}\)

The second angle of a triangle is \(3\) times as large as the first angle. The third angle is \(30\) degrees more than the first angle. Find the measure of the angles.

Exercise \(\PageIndex{21}\)

The second angle of a triangle is twice as large as the first. The measure of the third angle is \(20\) degrees greater than the first. How large are the angles?

Exercise \(\PageIndex{22}\)

The second angle of a triangle is three times as large as the first. The measure of the third angle is \(40\) degrees greater than that of the first angle. How large are the three angles?

Exercise \(\PageIndex{23}\)

The second angle of a triangle is five times as large as the first. The measure of the third angle is \(12\) degrees greater than that of the first angle. How large are the angles?

Exercise \(\PageIndex{24}\)

The second angle of a triangle is three times the first, and the third is \(12\) degrees less than twice the first. Find the measures of the angles.

Exercise \(\PageIndex{25}\)

The second angle of a triangle is four times the first and the third is \(5\) degrees more than twice the first. Find the measures of the angles.

Exercise \(\PageIndex{26}\)

The perimeter of a rectangle is \(150\) cm. The length is \(15\) cm greater than the width. Find the dimensions.

Exercise \(\PageIndex{27}\)

The perimeter of a rectangle is \(304\) cm. The length is \(40\) cm longer than the width. Find the length and width.

Exercise \(\PageIndex{28}\)

The perimeter of a rectangle is \(152\) meters. The width is \(22\) meters less than the length. Find the length and width.

Exercise \(\PageIndex{29}\)

The perimeter of a rectangle is \(280\) meters. The width is \(26\) meters less than the length. Find the length and width.

Exercise \(\PageIndex{30}\)

The perimeter of a college basketball court is \(96\) meters and the length is \(14\) meters more than the width. What are the dimensions?

Exercise \(\PageIndex{31}\)

A is \(60\) miles from B. An automobile at A starts for B at the rate of \(20\) miles per hour at the same time that an automobile at B starts for A at the rate of \(25\) miles an hour. How long will it be before the automobiles meet?

Exercise \(\PageIndex{32}\)

Two automobiles are \(276\) miles apart and start at the same time to travel toward each other. They travel at rates differing by \(5\) miles per hour. If they meet after \(6\) hours, find each rate.

Exercise \(\PageIndex{33}\)

Two trains travel toward each other from points which are \(195\) miles apart. They travel at rate of \(25\) and \(40\) miles an hour, respectively. If they start traveling at the same time, how long before the trains will meet?

Exercise \(\PageIndex{34}\)

Car A and Car B start traveling towards each other at the same time from points \(150\) miles apart. If Car A went at the rate of \(20\) miles an hour, at what rate must B travel if they meet in \(5\) hours?

Exercise \(\PageIndex{35}\)

A passenger and a freight train start toward each other at the same time from two points \(300\) miles apart. If the rate of the passenger train exceeds the rate of the freight train by \(15\) miles per hour, and they meet after \(4\) hours, what are the rates of the passenger and train?

Exercise \(\PageIndex{36}\)

Two automobiles started at the same time from a point, but traveled in opposite directions. Their rates were \(25\) and \(35\) miles per hour, respectively. After how many hours were they \(180\) miles apart?

Exercise \(\PageIndex{37}\)

A man having ten hours at his disposal made an excursion, riding out at the rate of \(10\) miles an hour and returning on foot at the rate of \(3\) miles an hour. Find the distance he rode.

Exercise \(\PageIndex{38}\)

A man walks at the rate of \(4\) miles per hour. How far can he walk into the country and ride back on a trolley that travels at the rate of \(20\) miles per hour if he must be back home \(3\) hours from the time he started?

Exercise \(\PageIndex{39}\)

A boy rides away from home in an automobile at the rate of \(28\) miles an hour and walks back at the rate of \(4\) miles an hour. The round trip requires \(2\) hours. How far does he ride in the automobile?

Exercise \(\PageIndex{40}\)

A motorboat leaves a harbor and travels at an average speed of \(15\) mph toward an island. The average speed on the return trip was \(10\) mph. How far was the island from the harbor if the total trip took \(5\) hours?

Exercise \(\PageIndex{41}\)

A family drove to a resort at an average speed of \(30\) mph and later returned over the same road at an average speed of \(50\) mph. Find the distance to the resort if the total driving time was \(8\) hours.

Exercise \(\PageIndex{42}\)

As part of his flight training, a student pilot was required to fly to an airport and then return. The average speed to the airport was \(90\) mph, and the average speed returning was \(120\) mph. Find the distance between the two airports if the total flying time was \(7\) hours.

Exercise \(\PageIndex{43}\)

Annie, who travels \(4\) miles an hour starts from a certain place \(2\) hours in advance of Brandie, who travels \(5\) miles an hour in the same direction. How many hours must Brandie travel to overtake Annie?

Exercise \(\PageIndex{44}\)

A man travels \(5\) miles an hour. After traveling for \(6\) hours another man starts at the same place following the first man at the rate of \(8\) miles an hour. When will the second man overtake the first man?

Exercise \(\PageIndex{45}\)

A motorboat leaves a harbor and travels at an average speed of \(8\) mph toward a small island. Two hours later a cabin cruiser leaves the same harbor and travels at an average speed of \(16\) mph toward the same island. In how many hours after the cabin cruiser leaves will the cabin cruiser be alongside the motorboat?

Exercise \(\PageIndex{46}\)

A long distance runner started on a course running at an average speed of \(6\) mph. One hour later, a second runner began the same course at an average speed of \(8\) mph. How long after the second runner started will the second runner overtake the first runner?

Exercise \(\PageIndex{47}\)

A car traveling at \(48\) mph overtakes a cyclist who, riding at \(12\) mph, has had a \(3\)-hour head start. How far from the starting point does the car overtake the cyclist?

Exercise \(\PageIndex{48}\)

A jet plane traveling at \(600\) mph overtakes a propeller-driven plane which has had a \(2\)-hour head start. The propeller-driven plane is traveling at \(200\) mph. How far from the starting point does the jet overtake the propeller-driven plane?

Exercise \(\PageIndex{49}\)

Two men are traveling in opposite directions at the rate of \(20\) and \(30\) miles per hour at the same time and from the same place. In how many hours will they be \(300\) miles apart?

Exercise \(\PageIndex{50}\)

Running at an average rate of \(8\) meters per second, a sprinter ran to the end of a track and then jogged back to the starting point at an average rate of \(3\) meters per second. The sprinter took \(55\) seconds to run to the end of the track and jog back. Find the length of the track.

Exercise \(\PageIndex{51}\)

A motorboat leaves a harbor and travels at an average speed of \(18\) mph to an island. The average speed on the return trip was \(12\) mph. How far was the island from the harbor if the total trip took \(5\) hours?

Exercise \(\PageIndex{52}\)

A motorboat leaves a harbor and travels at an average speed of \(9\) mph toward a small island. Two hours later a cabin cruiser leaves the same harbor and travels at an average speed of \(18\) mph toward the same island. In how many hours after the cabin cruiser leaves will the cabin cruiser be alongside the motorboat?

Exercise \(\PageIndex{53}\)

A jet plane traveling at \(570\) mph overtakes a propeller-driven plane that has had a \(2\)-hour head start. The propeller-driven plane is traveling at \(190\) mph. How far from the starting point does the jet overtake the propeller-driven plane?

Exercise \(\PageIndex{54}\)

Two trains start at the same time from the same place and travel in opposite directions. If the rate of one is \(6\) miles per hour more than the rate of the other and they are \(168\) miles apart at the end of \(4\) hours, what is each rate?

Exercise \(\PageIndex{55}\)

As part of flight training, a student pilot was required to fly to an airport and then return. The average speed on the way to the airport was \(100\) mph, and the average speed returning was \(150\) mph. Find the distance between the two airports if the total flight time was \(5\) hours.

Exercise \(\PageIndex{56}\)

Two cyclists start from the same point and ride in opposite directions. One cyclist rides twice as fast as the other. In three hours they are \(72\) miles apart. Find the rate of each cyclist.

Exercise \(\PageIndex{57}\)

A car traveling at \(56\) mph overtakes a cyclist who, riding at \(14\) mph, has had a \(3\)-hour head start. How far from the starting point does the car overtake the cyclist?

Exercise \(\PageIndex{58}\)

Two small planes start from the same point and fly in opposite directions. The first plane is flying \(25\) mph slower than the second plane. In two hours, the planes are \(430\) miles apart. Find the rate of each plane.

Exercise \(\PageIndex{59}\)

A bus traveling at a rate of \(60\) mph overtakes a car traveling at a rate of \(45\) mph. If the car had a \(1\)-hour head start, how far from the starting point does the bus overtake the car?

Exercise \(\PageIndex{60}\)

Two small planes start from the same point and fly in opposite directions. The first plane is flying \(25\) mph slower than the second plane. In \(2\) hours, the planes are \(470\) mi apart. Find the rate of each plane.

Exercise \(\PageIndex{61}\)

A truck leaves a depot at \(11\) a.m. and travels at a speed of \(45\) mph. At noon, a van leaves the same place and travels the same route at a speed of \(65\) mph. At what time does the van overtake the truck?

Exercise \(\PageIndex{62}\)

A family drove to a resort at an average speed of \(25\) mph and later returned over the same road at an average speed of \(40\) mph. Find the distance to the resort if the total driving time was \(13\) hours.

Exercise \(\PageIndex{63}\)

Three campers left their campsite by canoe and paddled downstream at an average rate of \(10\) mph. They then turned around and paddled back upstream at an average rate of \(5\) mph to return to their campsite. How long did it take the campers to canoe downstream if the total trip took \(1\) hour?

Exercise \(\PageIndex{64}\)

A motorcycle breaks down and the rider has to walk the rest of the way to work. The motorcycle was being driven at \(45\) mph, and the rider walks at a speed of \(6\) mph. The distance from home to work is \(25\) miles, and the total time for the trip was \(2\) hours. How far did the motorcycle go before it broke down?

Exercise \(\PageIndex{65}\)

A student walks and jogs to college each day. The student averages \(5\) kilometers per hour walking and \(9\) kilometers per hour jogging. The distance from home to college is \(8\) kilometers, and the student makes the trip in one hour. How far does the student jog?

Exercise \(\PageIndex{66}\)

On a \(130\)-mile trip, a car traveled at an average speed of \(55\) mph and then reduced its speed to \(40\) mph for the remainder of the trip. The trip took a total of \(2.5\) hours. For how long did the car travel at \(40\) mph?

Exercise \(\PageIndex{67}\)

On a \(220\)-mile trip, a car traveled at an average speed of \(50\) mph and then reduced its average speed to \(35\) mph for the remainder of the trip. The trip took a total of \(5\) hours. How long did the car travel at each speed?

Exercise \(\PageIndex{68}\)

An executive drove from home at an average speed of \(40\) mph to an airport where a helicopter was waiting. The executive boarded the helicopter and flew to the corporate offices at and average speed of \(60\) mph. The entire distance was \(150\) miles. The entire trip took \(3\) hours. Find the distance from the airport to the corporate offices.

How Do You Solve an Opposite-Direction Travel Problem?

Two people leave a location at different times and travel in opposite directions. What time will they be a certain distance apart? This tutorial takes you step-by-step through this classic word problem!

• word problem
• translate words to algebra
• uniform motion
• multiple step problem
• two equations
• constant speed
• rate times time
• 2 equations 2 unknowns
• solve by substitution
• two objects
• objects moving apart
• solve with two operations
• distributive property

Background Tutorials

Evaluating expressions.

What is a Variable?

You can't do algebra without working with variables, but variables can be confusing. If you've ever wondered what variables are, then this tutorial is for you!

Simplifying Expressions

What are Like Terms?

Combining like terms together is a key part of simplifying mathematical expressions, so check out this tutorial to see how you can easily pick out like terms from an expression

Solving Equations by Dividing

How Do You Solve an Equation Using Division?

Solving an equation for a variable? Perform the order of operations in reverse! Check it out in this tutorial.

Solving Two-Step Equations

How Do You Solve a Two-Step Equation?

Solving multi-step equations.

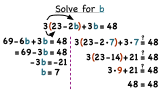
How Do You Solve a Multi-Step Equation Using the Distributive Property?

Trying to solve an equation where you see the same variable more than once? Figure out how to get those variables together and solve the equation with this tutorial!

Using Formulas

What's the Formula Connecting Distance, Speed, and Time?

When you have constant speed, the same formula pops up over and over again, and that's the formula that connects distance, speed, and time. Make sure you know this formula, and if you want a refresher, check out the tutorial!

Further Exploration

How Do You Figure Out the Time Traveled if You Know the Distance and Speed?

This tutorial provides a great real world application of math. You'll see how to use uniform motion to figure out how long it will take to go a certain distance traveling at a constant speed. Check it out!

How Do You Figure Out the Rate Traveled if You Know the Distance and Time?

This tutorial provides a great real world application of math! Follow along with this tutorial to figure out how fast you need to go to travel a certain distance in a certain amount of time.

• Terms of Use

When it comes to math, maybe the kids aren’t the problem

The way we are teaching, testing, and requiring mathematics is damaging our society with potentially fatal results. That’s a strong statement, I know, but to get a sense of why, take a moment to think of something that you would find hard or maybe impossible to do — executing 30 pullups, playing a violin concerto, walking a tightrope over an abyss, feeding a snake, solving a complex polynomial equation. 

Now suppose our society decrees that to graduate from high school, you must be able to do that thing or be branded a failure and not earn a diploma. How are you feeling about yourself and your prospects?

Imagine trying your hardest to learn the skills, but the textbooks, online resources and sometimes even teachers confuse you, and on top of that, some exams are so badly designed they are virtually impossible to pass. 

The 2022 results from the National Assessment of Educational Progress showed only 36% of fourth graders and 26% of eighth graders were considered proficient in mathematics. The national average for high school math proficiency is just 38%.

Why are so many young people not achieving math proficiency? Consider how we define “proficiency.” 

For example, the Common Core math standards state that, among other things, high school students should “Recognize that sequences are functions, sometimes defined recursively, whose domain is a subset of the integers. For example, the Fibonacci sequence is defined recursively by f (0) = f (1) = 1, f (n+1) = f (n) + f (n-1) for n ≥ 1.” And that’s just one example of many.

Suppose your child came to you with that as homework each night, possibly in tears. Now imagine that your child has special needs and deals with dyscalculia , ADD or other challenges.  

One of my sons struggles with ADD and is trying to complete an online financial algebra course offered by his school district to fulfill his mandatory “math pathway” for graduation. To help him succeed, a certified math and science tutor and I have worked with him every day through some very poorly designed online lessons provided by his district. 

We also helped him try to solve problems during a unit exam, but together, we achieved only a score of 32% on the exam. A certified math teacher, and a former statistics instructor with a Ph.D., failed a high school financial algebra exam. Why? Because the lessons were deeply flawed, the exam items were ambiguously worded, there were too many problems for the allotted time and the rules prohibited the use of resources like a financial calculator that one might enlist in real life. 

All that is not an excuse, and this column is not some reflexive “anti-testing” rant. It is, unfortunately, the truth. That leaves us asking, “If we failed the exam, how will most students, or their parents, possibly succeed?”

If you make children and their parents feel like failures, it is predictable that some are eventually going to give up on school and on themselves. Once that happens, they are far more likely to turn to behaviors that are harmful, self-destructive, and, tragically, sometimes fatal. And when significant portions of our population share those feelings, it inevitably harms our society as a whole. It is nothing less than educational and social malpractice to create unrealistic and unnecessary demands for children and then fail to provide them with the best resources to help them succeed.   

A good start would be to insist that policymakers, superintendents, school boards and school principals throughout our state attempt to learn each subject in math through the same texts or online resources students are required to use. I don’t mean just skimming a text or taking the word of someone else, I mean really digging in and trying to learn the material and take the tests firsthand. I doubt most people would accept the challenge and I am certain even fewer would pass the exams. 

That is not because the administrators and teachers aren’t smart, good people — it is because the materials and exams are so poorly designed, and the requirements are so profoundly detached from daily life. But if that is so, which the evidence suggests it is, why are we inflicting such things on our children and with what impacts?

Most Read Opinion Stories

• The U.S. Supreme Court released a code of ethics. Here's what's missing
• Dismantling highly capable cohorts will hurt all students
• Before you drop that scooter, think about who else uses the sidewalk
• It's time to make the climate just as central as DEI in everything we do
• The 4-day work week is decades away

The opinions expressed in reader comments are those of the author only and do not reflect the opinions of The Seattle Times.

Live eclipse traffic: Heavy traffic building in central Ohio as travelers return south

Traffic along north and west Columbus remains heavy at 6 p.m. Monday as motorists make their way home from viewing the solar eclipse.

The heaviest traffic is U.S. 33 eastbound between Dublin and Marysville, and there are backups along southbound Interstate 71 north of Columbus and on I-70 west of the city, according to the Ohio Department of Transportation (ODOT).

Solar Eclipse 2024 live updates: Ohio traffic begins to slow; several state parks already at capacity

Here's what to know as travelers return following the eclipse:

Live traffic updates: traffic building, crash on U.S. 33 as travelers return south

The slowest travel at 6 p.m. is U.S. 33 between Marysville and Dublin as travelers make their way back to Columbus following the eclipse, according to ODOT.

A crash that blocked an eastbound lane of U.S. 33 in Marysville also was slowing traffic.

Travelers can expect up to a 30-minute delay between Marysville and Dublin along 33, according to ODOT.

Traffic is heavy elsewhere in the region, including the eastbound lanes of Interstate 70 west of Columbus and the southbound lanes of I-71 north of I-270. Both areas reported 10-minute delays.

Separately, a disabled vehicle caused backups in the eastbound lanes of I-270 on the South Side, causing delays of about 15 minutes.

There was also a crash that closed the shoulders on I-270 south of Roberts Road that slowed traffic.

ODOT to eclipse travelers: Brace for slow return home

While the pace of traffic to the eclipse has been slow to build, ODOT spokesperson Matt Bruning urged people to prepare for a long return time as everyone who headed to the path of totality tries to get home.

“Patience will be key for sure, if you can stay put the longer you can after the event the easier it will be,” Bruning said. “History is a teacher, and it teaches that is not what happens, everyone leaves and wants to get home at the same time.”

North central Ohio saw slowdowns on routes to eclipse

In addition to heavy traffic on U.S. 33, ODOT's traffic cameras also showed heavy traffic on Ohio 315 near the Franklin-Delaware County line and the Ohio 315 and U.S. 23 interchange. The two left lanes of I-270 west were also closed at State Route 315 south due to a crash.

Traffic along Interstate 71 in Delaware County was also heavy near Alum Creek State Park.

Roadways in Powell near the Columbus Zoo and Aquarium were also seeing increased traffic and slowdowns.

On the East Side of Columbus, a ramp from Interstate 670 to U.S. 62 was closed in both directions due to a crash, but is now reopened.

How to check live traffic, see road cameras in Ohio

The ODOT OHGO website has live traffic updates, as well as access to dozens of traffic cameras throughout the state to make informed traveling decisions before heading out.

ODOT: Do not watch eclipse from side of highway

Bruning also said to be mindful of ODOT and state law enforcement workers, and said it was not legal for drivers to stop on the highway to watch the eclipse.

@Colebehr_report

[email protected]

Traffic delays and other issues mark total solar eclipse day

Authorities on Monday reported traffic crashes and significant road delays across the country as thousands of people flocked to prime locations to gaze up at the rare solar eclipse – and then made their way home again.

Local roads and highways in states including Texas, Ohio, Illinois, Michigan, Indiana, Vermont and New Hampshire were impacted by the flood of drivers, many of whom were from out of state. The most intense bottlenecks appeared to be in the path of totality , a vast swath of the country – approximately 115 miles wide, crossing through 13 states – where people were able to view the total eclipse.

Traffic slowed on major highways in Indiana as the eclipse progressed Monday afternoon. State transportation officials posted video showing backups forming on Interstate 65 headed toward Indianapolis, the Indianapolis Star reported. The Courier & Press in Evansville reported delays after the eclipse ended.

Indiana State Police Sgt. John Perrine posted on X that traffic on state highways was flowing but rest stops along interstates in the path of totality are at or near capacity. 

Perrine said transportation officials planned to shut them down "once they are full and will not allow any more traffic in for the duration of the eclipse." One rest stop along I-74 near Veedersburg, northwest of Indianapolis, closed because it had reached maximum capacity from "eclipse viewing traffic." 

In Oklahoma, a crash around 7:30 a.m. local time narrowed eastbound lanes on I-40, a major transcontinental highway that runs from California to North Carolina. The crash occurred not far from several state parks that were hosting eclipse events, and was within driving distance of the full eclipse path, which included parts of southeastern Oklahoma and Arkansas.

"Crews estimate cleanup will take the majority of the day. Expect delays in the area and use extra caution. #trucking #eclipse," said a post on X by the Oklahoma Department of Transportation .

Multiple crashes were reported in Waco, Texas, a city in the path of totality, which hosted several festivities and eclipse viewing events. The crashes all occurred on I-35, which runs from southern Texas to Minnesota. The wrecks shut down multiple lanes.

"Expect major traffic delays in this area," the Texas Department of Transportation said in a statement around 9 a.m. local time.

Officials warn drivers of delays, dangers ahead of solar eclipse

In the weeks leading up to the celestial event, officials issued warnings about heavy traffic congestion and the danger of driving during the eclipse , including distracted pedestrians and the sudden change in light conditions. Eclipses have previously been tied with surges in traffic crashes, including fatal collisions.

In New York, extra troopers were staged throughout the entire state, especially in northern counties and cities, such as Buffalo, from which spectators can see a full eclipse, according to the New York State Police .

In Ohio, the state's Turnpike and Infrastructure Commission heavily staffed its toll booths, service plazas and maintenance buildings in anticipation of the eclipse, which it has designated as "a high-volume traffic event" like, for example, Thanksgiving.  The Ohio Emergency Management Agency estimates, for the solar eclipse, between 150,000 and 575,000 travelers will visit the state, which encompasses areas in the path of totality.

During the 2017 eclipse, congestion in some areas lasted for up to 13 hours after totality,  according to Transportation Research News , a National Research Council publication. An analysis of traffic patterns from that year suggests the worst of the traffic – on interstates and rural back roads alike – will kick off after the eclipse ends and everyone tries to leave all at once.

Contributing: Kayla Jimenez and Phaedra Trethan, USA TODAY ; The Indianapolis Star

Low dangling traffic light closes Weymouth highway ramp

WEYMOUTH, MASS. (WHDH) - The ramp from Route 3 South to Route 18 in Weymouth was closed for a few hours Friday due to a line of traffic lights dangling low above the road.

Traffic was backed up for miles during the evening commute, and Weymouth Mayor Bob Hedlund said he believes a very high truck caught the wires and took the traffic lights down. The driver has not been located.

“We’ve never seen a disruption as bad as this,” Hedlund said. “My planning department director lives right on Route 18 at that intersection and he had some difficulty getting home tonight.”

While repair crews took down damaged wires and strung the signals back up, neighboring police departments sent in officers to direct traffic.

Although the traffic disruption took place about a block from South Shore Hospital, ambulances were still able to get to the hospital as usual.

Advisory: Closure of Ramp from Route 3 SB to Route 18 in #Weymouth for emergency signal repairs. This closure is expected to be in place for approximately three to four hours. pic.twitter.com/cD0OBv1j09 — Mass. Transportation (@MassDOT) April 12, 2024

(Copyright (c) 2024 Sunbeam Television. The Associated Press contributed to this report. All Rights Reserved. This material may not be published, broadcast, rewritten, or redistributed.)

• 7WEATHER: Spotty Showers Saturday
• Running group sues Boston Marathon and Newton Police for alleged racial profiling
• Israel threatens to strike Iran directly if Iran launches attack from its territory
• 1 dead and 13 injured in semitrailer crash at a Texas public safety office, with the driver jailed

Word Problems: Travel and Distance Lessons

Right-Wing Media Are in Trouble

As you may have heard, mainstream news organizations are facing a financial crisis. Many liberal publications have taken an even more severe beating. But the most dramatic declines over the past few years belong to conservative and right-wing sites. The flow of traffic to Donald Trump’s most loyal digital-media boosters isn’t just slowing, as in the rest of the industry; it’s utterly collapsing.

This past February, readership of the 10 largest conservative websites was down 40 percent compared with the same month in 2020, according to The Righting , a newsletter that uses monthly data from Comscore—essentially the Nielsen ratings of the internet—to track right-wing media. (February is the most recent month with available Comscore data.) Some of the bigger names in the field have been pummeled the hardest: The Daily Caller lost 57 percent of its audience; Drudge Report , the granddaddy of conservative aggregation, was down 81 percent; and The Federalist , founded just over a decade ago, lost a staggering 91 percent. (The site’s CEO and co-founder, Sean Davis, called that figure “laughably inaccurate” in an email but offered no further explanation.) FoxNews.com, by far the most popular conservative-news site, has fared better, losing “only” 22 percent of traffic, which translates to 23 million fewer monthly site visitors compared with four years ago.

Some amount of the decline over that period was probably inevitable, given that 2020 was one of the most intense and newsiest years in decades, propping up publications across the political spectrum. But that doesn’t explain why the falloff has been especially steep on the right side of the media aisle.

What’s going on? The obvious culprit is Facebook. For years, Facebook’s mysterious algorithms served up links to news and commentary articles, sending droves of traffic to their publishers. But those days are gone. Amid criticism from elected officials and academics who said the social-media giant was spreading hate speech and harmful misinformation, including Russian propaganda, before the 2016 election, Facebook apparently came to question the value of featuring news on its platform. In early 2018, it began deemphasizing news content, giving greater priority to content posted by friends and family members. In 2021, it tightened the tap a little further. This past February, it announced that it would do the same on Instagram and Threads. All of this monkeying with the internet’s plumbing drastically reduced the referral traffic flowing to news and commentary sites. The changes have affected everyone involved in digital media, including some liberal-leaning sites—such as Slate (which saw a 42 percent traffic drop), the Daily Beast (41 percent), and Vox (62 percent, after losing its two most prominent writers)—but the impact appears to have been the worst, on average, for conservative media. (Referral traffic from Google has also declined over the past few years, but far less sharply.)

[ Adrienne LaFrance: Mark Zuckerberg doesn’t understand journalism ]   

Unsurprisingly, the people who run conservative outlets see this as straightforward proof that Big Tech is trying to silence them. Neil Patel, a co-founder (with Tucker Carlson) of the Daily Caller , told me that the tech giants want “to crush any independent media that was perceived to have been helpful to Trump’s rise.” Patel calls this a form of “Big Tech–driven viewpoint discrimination” that “should scare any fair-minded individual.”

A simpler explanation is that conservative digital media are disproportionately dependent on social-media referrals in the first place. Many mainstream publications have long-established brand names, large newsrooms to churn out copy, and, in a few cases, large numbers of loyal subscribers. Sites like Breitbart and Ben Shapiro’s The Daily Wire , however, were essentially Facebook-virality machines, adept at injecting irresistibly outrageous, clickable nuggets into people’s feeds. So the drying-up of referrals hit these publications much harder.

And so far, unlike some publications that have pivoted away from relying on traffic and programmatic advertising, they’ve struggled to adapt. Rather than stabilizing amid Facebook’s new world order, traffic on the right has mostly continued south. Among the big losers over the past year are The Washington Free Beacon , whose traffic was down 58 percent, and Gateway Pundit, down 62 percent. Compare that with prominent mainstream and liberal sites, which, although still well below their 2020 heights, have at least stanched the bleeding. Traffic to The Washington Post and The New York Times from February 2023 to February 2024 was essentially flat. Slate ’s was up 14 percent.

For conservative media publishers, the financial consequences of such a steep decline in readership are hard to know for certain. None of the best-known names publicly reports revenue figures, and many are supported by rich patrons who may not be in it for the money. But the situation can’t be good. Digital media still rely on advertising, and advertising still goes to places with more, not fewer, people paying attention. Traffic also drives subscriptions.

More broadly, the loss of readership can’t be helpful to the ideological cause. Top-drawing sites like the conspiratorial Gateway Pundit and Infowars help keep the MAGA faithful faithful by recirculating, amplifying, and sometimes creating the culture-war memes and talking points that dominate right and far-right opinion. Less traffic means less influence.

[ Paul Farhi: Is American journalism headed toward an ‘extinction-level event’? ]

The Daily Caller ’s Patel insisted that faltering traffic alone isn’t a death sentence for the onetime lords of the conservative web. With the addition of a subscription service and tighter financial management, the Daily Caller ’s financial health is solid and improving, he said. Outlets like his own can still succeed with people who “have lost trust in the corporate media and are actively seeking alternatives.”

The trouble is that there are now alternatives to the alternatives. The Righting’s proprietor, Howard Polskin, pointed out to me that the websites that dominated the field in 2016—Fox News, Breitbart, The Washington Times , and so on—are no longer the only players in MAGA world. The marketplace has expanded and fragmented since then, splintering the audience seeking conservative or even extremist perspectives among podcasts, YouTube videos, Substack newsletters, and boutique platforms like Rumble. “There’s a lot of choice,” Polskin said. “Even if [the big] sites went out of business tomorrow, there are a lot of voices still out there.”

The DIY ethic is embodied by the likes of Megyn Kelly, Bill O’Reilly, Steve Bannon, and Carlson, who became conservative celebrities while working for established media organizations but have maintained their profiles after leaving them in disgrace. Since being fired by Fox News last year, Carlson has moved his contentious commentaries and interviews (including one with Vladimir Putin) to X. Kelly has come back from a messy divorce with NBC in 2019 (which followed an unhappy exit from Fox News in 2017) to host a massively popular podcast. O’Reilly, likewise forced out of Fox in 2017, has kept talking via newsletters, video streams, and weekly appearances on the NewsNation cable channel. And Bannon, the former Trump consigliere who left Breitbart , which he founded, after publicly criticizing the Trump family, has gone the podcaster route himself; his War Room podcast was ranked as the leading source of false and misleading information in a broad study of the medium by the Brookings Institution last year.

The precipitous decline in traffic to conservative publications raises a larger and possibly unanswerable question: Did these operations ever really hold the political and cultural clout that critics ascribed to them at their peak? Recall the liberal anger in 2020 when Ben Shapiro was routinely dominating Facebook’s most-engaged content list, generating accusations that Facebook’s algorithm was favoring right-wing posts and pushing voters toward Trump. Yet Joe Biden went on to win the election easily, and Democrats overperformed in the 2022 midterms. Now, as conservatives cry that Big Tech has crushed their traffic, Trump is running neck and neck with Biden in the polls, even with a legal cloud hanging over him and shortfalls of campaign cash. Maybe who wins the traffic contest doesn’t matter as much as it once appeared.